W tym poście postaram się pokazać drogę tworzenia modelu konwolucyjnej sieci neuronowej do klasyfikacji samochodów wg. marki, modelu i rocznika. Zacznę od analizy zbioru danych, potem porównam model z jednym i z trzema wyjściami, skorzystam z tf.data i learning rate warm-up do poprawy działania modelu, a na koniec porównam działanie sieci własnej – prostej CNN z modelem EfficientNet.
Dla osób zainteresowanych kodem – wszystko jest dostępne tutaj.
Bazy danych
Aktualnie kilka baz danych, zawierających opisane zdjęcia samochodów, jest dostępnych bezpłatnie. Zbiory różnią się liczebnością (od kilku do kilkuset tysięcy zdjęć), niektóre zawierają wyłącznie zdjęcia z jednego kierunku (np. z tyłu lub z góry). Są również zbiory zawierające elementy samochodów lub ich wnętrza.
Przykłady zbiorów można znaleźć np. na tych stronach:
- https://www.gti.ssr.upm.es/data/Vehicle_database.html
- https://ai.stanford.edu/~jkrause/cars/car_dataset.html (cars196 w TF datasets)
- http://vmmrdb.cecsresearch.org (z opisami)
Oprócz tego istnieją również zbiory płatne, zawierające np. zdjęcia samochodów z wyciętym tłem i zdjęcia 360 stopni.
Analiza zbioru
Zanim rozpocznę tworzenie modelu zapoznam się dokładniej z danymi. Pomoże mi w tym oczywiście oglądanie obrazów ze zbioru, ale również histogramy.

Ile jest przykładów w klasach?
Sprawdźmy jak wygląda rozkład zdjęć na klasy dla marki, modelu i rocznika. W tym celu wykorzystamy poniższy fragment kodu – przykład dla marki.
make_hist = [0] * len(CLASS_NAMES_MAKE)
for marka in make:
make_hist[np.where(CLASS_NAMES_MAKE == marka)[0][0]] += 1
d = {'nazwa': CLASS_NAMES_MAKE, 'images_nr': make_hist}
df = pd.DataFrame(data=d)
df = df.sort_values('images_nr', ascending=False)
fig, ax = plt.subplots(figsize = (20,15))
sns.barplot(ax=ax, x='nazwa', y='images_nr', data = df, palette=sns.color_palette("gist_earth", n_colors=len(CLASS_NAMES_MAKE)))
ax.set_xticklabels(ax.get_xticklabels(), rotation=45, horizontalalignment='right')
ax.set(xlabel="Marka", ylabel='Liczba zdjęć')
ax.tick_params(axis='y', labelsize = 15)
ax.tick_params(axis='x', labelsize = 12)
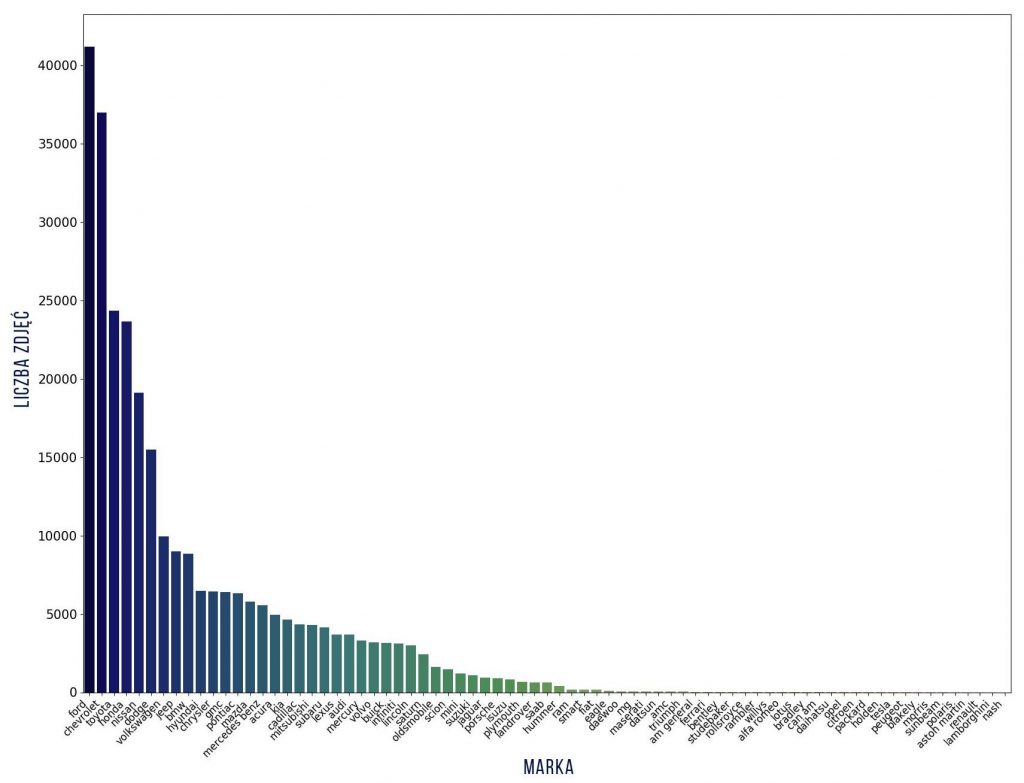
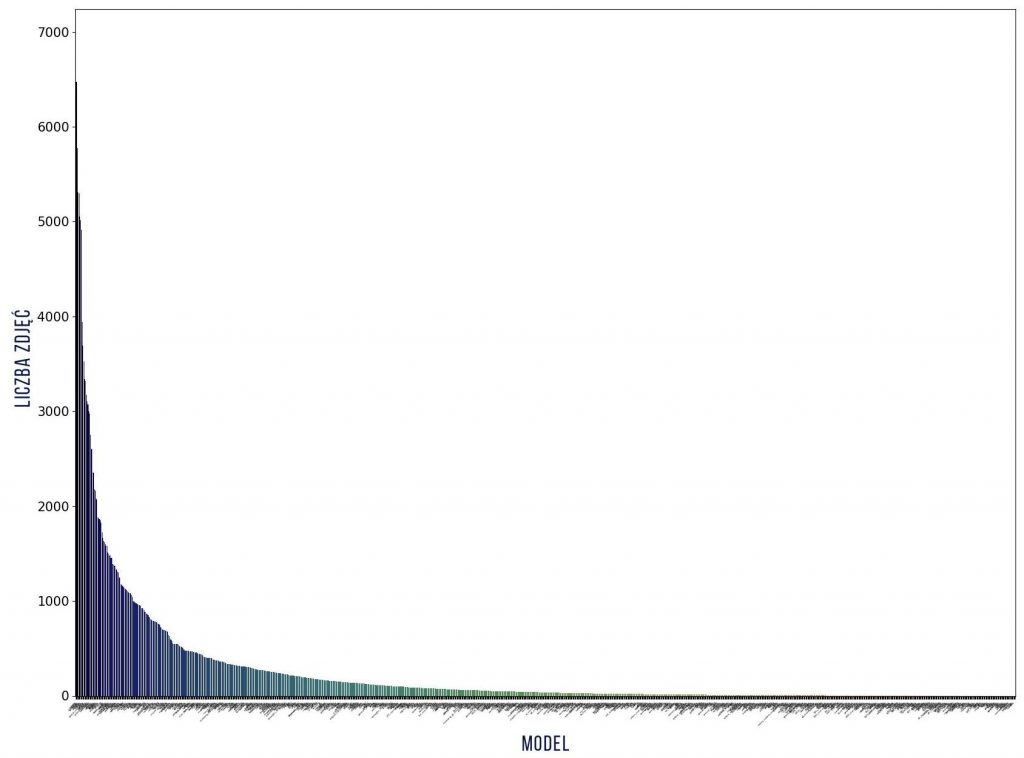
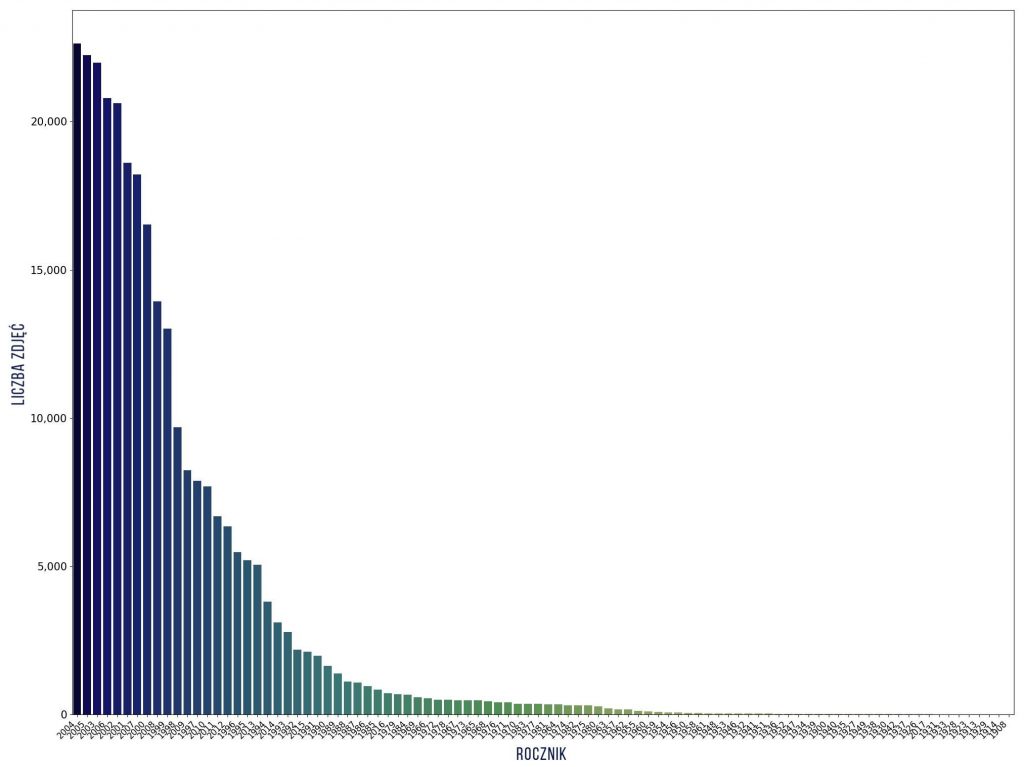
Jak widać liczności klas różnią się – od 1 do ponad 6 tys. zdjęć dla każdego modelu, dlatego wybiorę tylko te klasy, które mają co najmniej 100 zdjęć, natomiast najliczniejsze klasy ograniczę do maksymalnie 200 zdjęć. W wyniku tych ograniczeń otrzymałam histogramy o bardziej wyrównanej liczności w klasach (przy tych ograniczeniach klasę rozumiem jako trójkę: marka + model + rocznik). Nie dało to wyrównania liczebności oddzielnie – klas marek, modeli i roczników. Nazwy modeli nie istnieją w oderwaniu od marek, a pojazdy w roczniku mają niewiele podobnych cech (jest pewien styl, ale i tak połączmy te cechy).
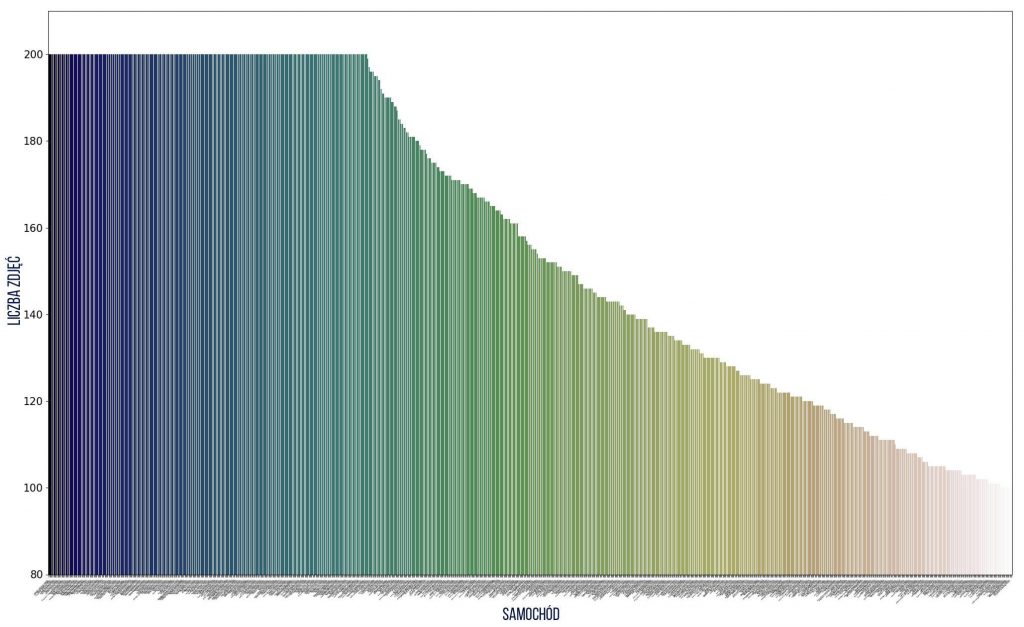
Jak wyglądają samochody?
Sprawdźmy jak wyglądają zdjęcia różnych samochodów, które należą do tej samej klasy. Poniżej funkcja którą wykorzystuję do rysowania oraz przykładowe wyniki dla:
- wszystkich samochodów marki Audi
- wszystkich modeli Civic
- wszystkich samochodów z roku 1999
def plot_images(dataset, rows, columns, chosen):
output = np.zeros((IMG_SIZE * columns, IMG_SIZE * rows, 3))
row = 0
column = 0
for image, label in dataset:
if np.argmax(label[1].numpy()) == chosen:
output[column*IMG_SIZE:(column+1)*IMG_SIZE, row*IMG_SIZE:(row+1)*IMG_SIZE] = image.numpy()
column += 1
if column >= columns:
column = 0
row += 1
if row >= rows:
break
plt.figure(figsize=(20,16))
plt.imshow(output)
plt.show()



Dzięki tej wizualizacji widzimi jak bardzo różnorodne zdjęcia znajdują się w zbiorze. Różne kolory pojazów, fotografie z różnych stron, pod różnym kątem, przy różnym oświetleniu, na różnorodnym tle.
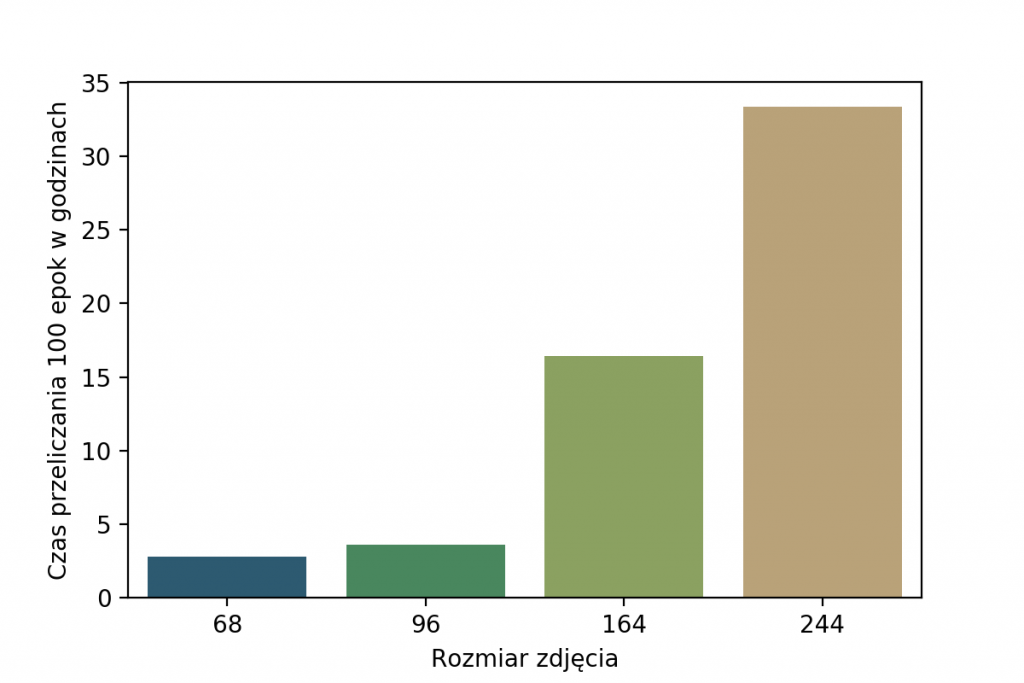
Oryginalne zdjęcia były w rozmiarach od 50×50 do 1686×560 pikseli. Po wstępnych testach z różnymi rozmiarami na wejściu sieci, wybrałam wymiar 96×96 pikseli. Taka zmiana skali oraz nierzadko również współczynnika kształtu wprowadza znaczne zniekształcenia. Czemu 96px, a nie więcej czy mniej? Spójrz na wyniki dokładności klasyfikacji poniżej, widać na nich, że najlepszy wybór to 244x244px.
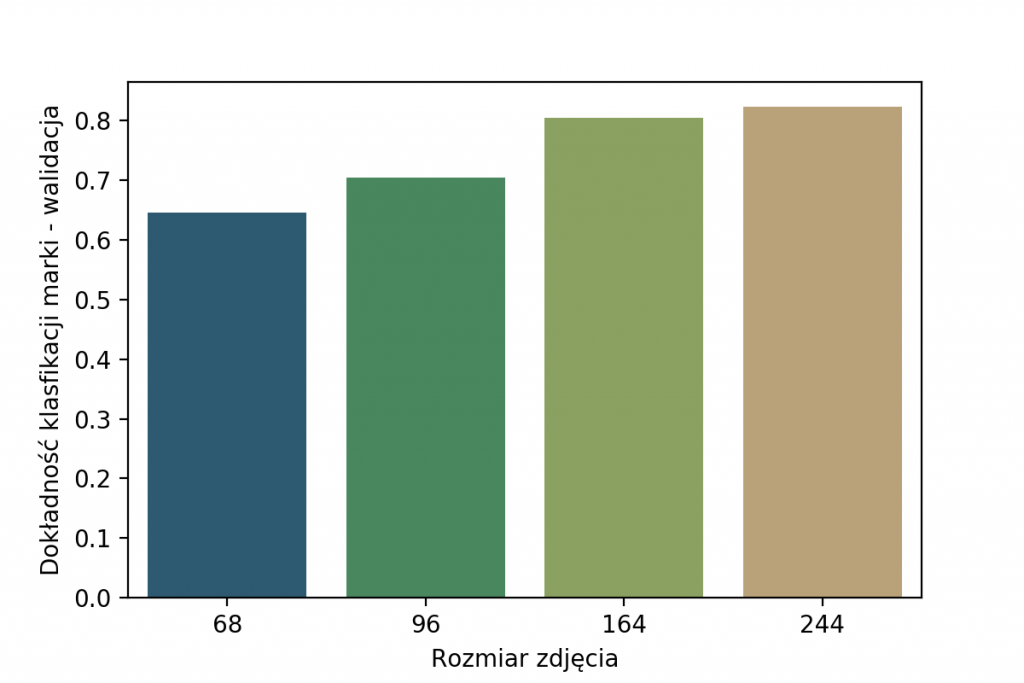
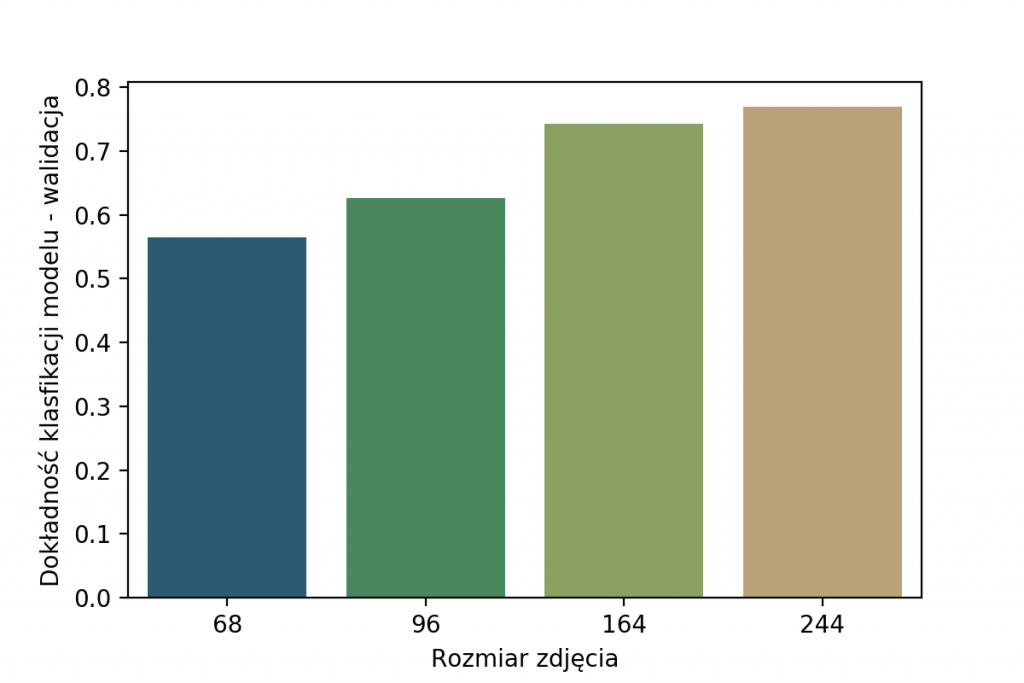
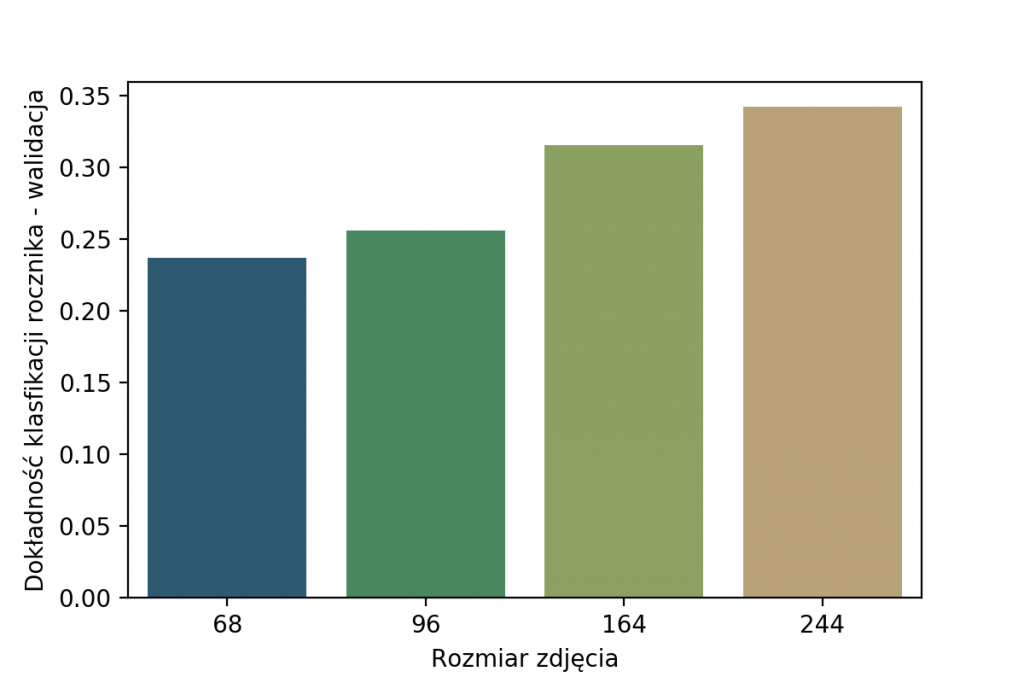
Dlaczego w takim razie 96×96, skoro można uzyskać znacznie lepsze wyniki? Powód jest prosty – znacznie dłuższy trening w przypadku większych wejść. Widać to świetnie na poniższym wykresie, gdzie pokazuję czas trwania 100 epok treningu. Ze względu na fakt, że zależy nam na czasie (96px zamiast 244px to prawie 10x szybciej) wybrałam właśnie 96×96.
Wczytywanie danych – TensorFlow Data
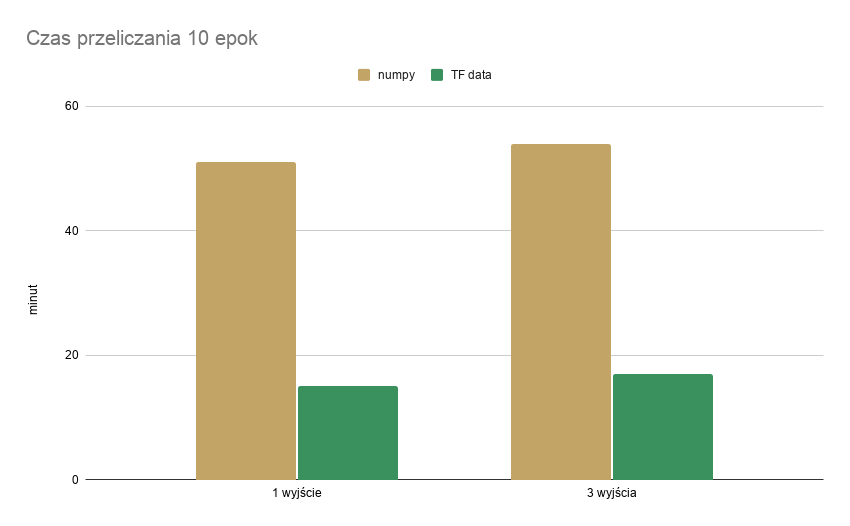
Rozpoczęłam od prostego modelu CNN z jednym wyjściem (marka), wczytując dane przez numpy.array, potem dodałam dwa pozostałe wyjścia. Ze względu na długi czas przetwarzania danych wejściowych zdecydowałam się na wykorzystanie tensorflow.data do przetwarzania i podawania do modelu danych – najpierw dla jednego wyjścia, następnie dla trzech. Porównanie czasów przeliczeń znajduje się w tabeli poniżej.
| numpy.array | tensorflow.data | |
| 1 wyjście | 51 min 46 sek | 15 min 0 sek |
| 3 wyjścia | 54 min 43 sek | 17 min 7 sek |
Ponadto czas przetwarzania danych (ok. 267 tys. zdjęć):
- numpy.array: 30 min 22 sek,
- tensorflow.data: 1,786 sek
Uwaga do powyższych: mój kod nie był optymalny, ale zastosowanie tensorflow.data było najprostszym i jak widać skutecznym) sposobem na przyspieszenie obliczeń. Dodatkowo zmnieszyło się zużycie RAM.
Poszukiwanie hiperparametrów
Wstępnie przeprowadzałam testy z arbitralnie ustalonymi parametrami (ten model będę nazywać 'pierwszym modelem’).
Szukanie najlepszych hiperparametrów modelu podzieliłam na 4 etapy. Wstępnie skorzystałam z parametrów wyznaczonych dla sieci z tego postu, następnie z pomocą Optuna dobierałam kolejno parametry:
- warstw konwolucyjnych (rozmiary kerneli i liczby neuronów),
- warstw dense (oddzielnie dla marki, modelu i rocznika),
- regularyzacji (L2 i dropout, również osobno dla każdego z wyjść).
Na każdym z etapów zostało sprawdzonych co najmniej 120 zestawów parametrów, w tym pierwszych 100 było losowe. Na koniec wyznaczyłam learning rate, korzystając z LR Scheduler.
Ostatecznie model wyglądał tak:
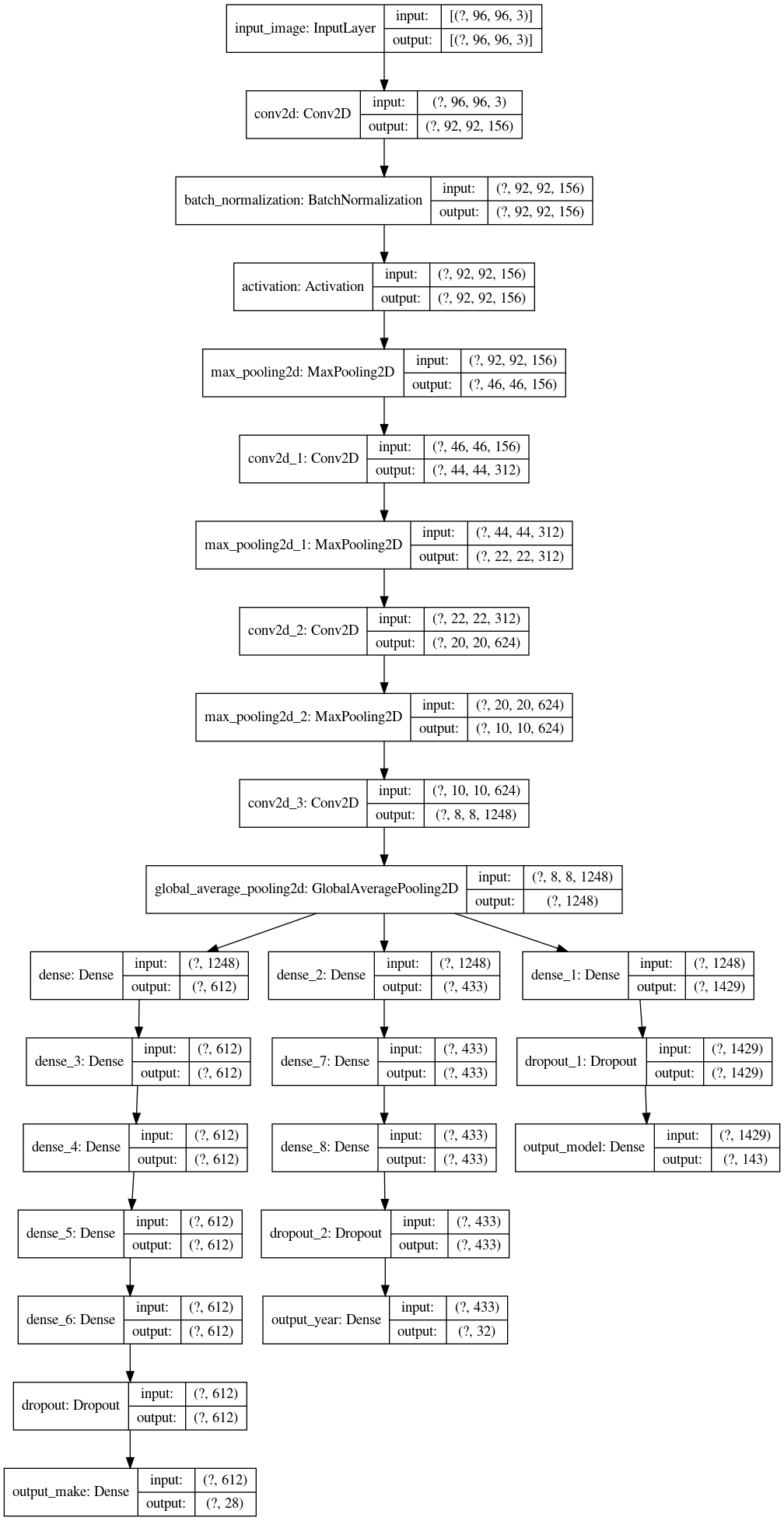
image_input = keras.Input(shape=(IMG_WIDTH, IMG_HEIGHT, 3), name='input_image')
x = layers.Conv2D(156, (5, 5), use_bias=False)(image_input)
x = layers.BatchNormalization()(x)
x = layers.Activation('relu')(x)
x = layers.MaxPooling2D()(x)
x = layers.Conv2D(312, (3, 3), activation='relu')(x)
x = layers.MaxPooling2D()(x)
x = layers.Conv2D(624, (3, 3), activation='relu')(x)
x = layers.MaxPooling2D()(x)
x = layers.Conv2D(1248, (3, 3), activation='relu')(x)
x = layers.GlobalAveragePooling2D()(x)
l2_make = tf.keras.regularizers.l2(7e-6)
l2_model = tf.keras.regularizers.l2(4.4e-6)
l2_year = tf.keras.regularizers.l2(9e-6)
l_make = layers.Dense(612, activation='relu', kernel_regularizer = l2_make)(x)
l_model = layers.Dense(1429, activation='relu', kernel_regularizer = l2_model)(x)
l_year = layers.Dense(433, activation='relu', kernel_regularizer = l2_year)(x)
for i in range(4):
l_make = layers.Dense(612, activation='relu', kernel_regularizer = l2_make)(l_make)
l_make = layers.Dropout(0.2)(l_make)
l_model = layers.Dropout(0.35)(l_model)
for i in range(2):
l_year = layers.Dense(433, activation='relu', kernel_regularizer = l2_year)(l_year)
l_year = layers.Dropout(0.25)(l_year)
output_make = layers.Dense(len(CLASS_NAMES_MAKE), activation='softmax', name='output_make')(l_make)
output_model = layers.Dense(len(CLASS_NAMES_MODEL), activation='softmax', name='output_model')(l_model)
output_year = layers.Dense(len(CLASS_NAMES_YEAR), activation='softmax', name='output_year')(l_year)
cnn = keras.Model(inputs=image_input, outputs=[output_make, output_model, output_year], name='cars_model')
cnn.compile(optimizer='Adam',
loss='categorical_crossentropy',
metrics=['acc'])
Data augmentation
Poprzez dodanie augmentacji, z niewielką zmianą koloru, nasycenia, jasności i kontrastu, ponadto losowe lustrzane odbicie i rotacja w granicach ± 10 stopni, zwiększyłam zbiór uczący. Poniżej przedstawione jest 5 zmodyfikowanych zdjęć dla różnych samochodów.

Podsumowanie wyników różnych modeli
Wyniki i wszystkie poniższe wizualizacje są dla 4 modeli:
- pierwszego model bez augmentacji,
- pierwszego modelu z augmentacją,
- ostatniego modelu z augmentacją,
- modelu z EfficientNetB1, z parametrami warstw dense dobranymi w tym poście, z augmentacją.
Augmentacja w tych modelach była jednakowa.
| Top 1 error rate (zbiór treningowy) | marka | model | rocznik |
| pierwszy model bez augmentacji | 0,05% | 0,08% | 0,31% |
| pierwszy model | 0,12% | 0,82% | 14,6% |
| ostatni model | 0,72% | 0,41% | 11,52% |
| model z EfficientNet | 1,89% | 3,71% | 55,76% |
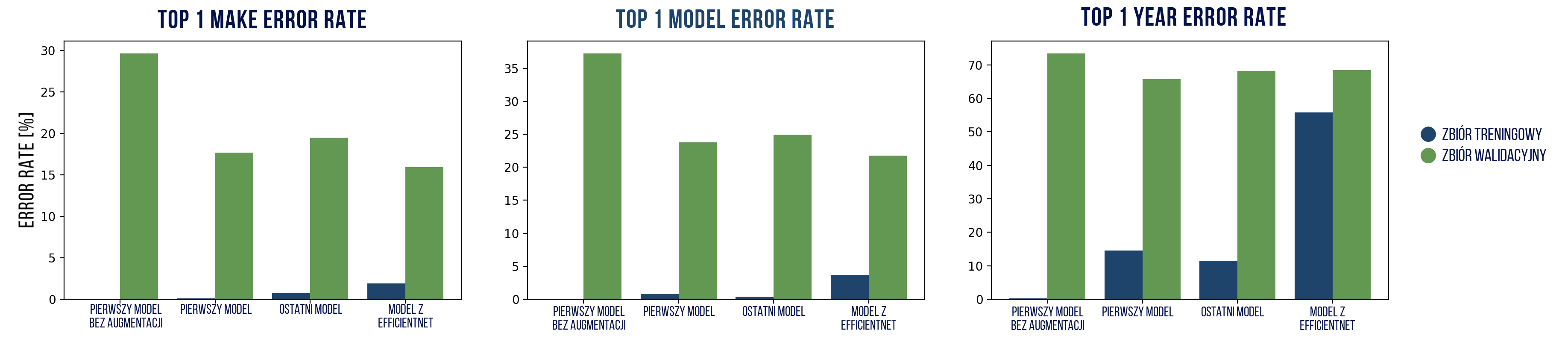
| Top 1 error rate (zbiór walidacyjny) | marka | model | rocznik |
| pierwszy model bez augmentacji | 29,67% | 37,25% | 73,43% |
| pierwszy model | 17,67% | 23,76% | 65,68% |
| ostatni model | 19,49% | 24,93% | 68,22% |
| model z EfficientNet | 15,95% | 21,79% | 68,4% |
| Top 5 error rate (zbiór treningowy) | marka | model | rocznik |
| pierwszy model bez augmentacji | 0,00% | 0,00% | 0,00% |
| pierwszy model | 0,00% | 0,00% | 0,16% |
| ostatni model | 0,01% | 0,00% | 0,10% |
| model z EfficientNet | 0,02% | 0,08% | 3,55% |
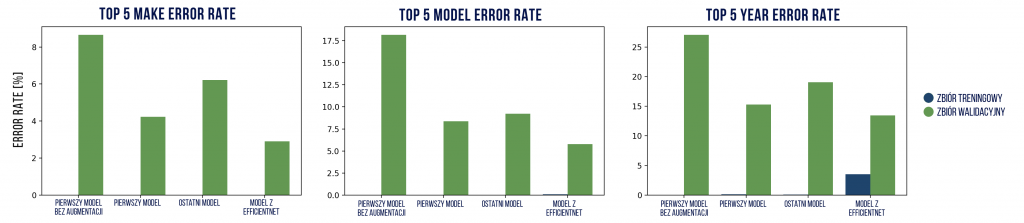
| Top 5 error rate (zbiór walidacyjny) | marka | model | rocznik |
| pierwszy model bez augmentacji | 8,66% | 18,17% | 27,06% |
| pierwszy model | 4,23% | 8,73% | 15,30% |
| ostatni model | 6,22% | 9,21% | 19,07% |
| model z EfficientNet | 2,91% | 5,77% | 13,47% |
Jak sieć podejmuje decyzje? czyli Class Activation Mapping
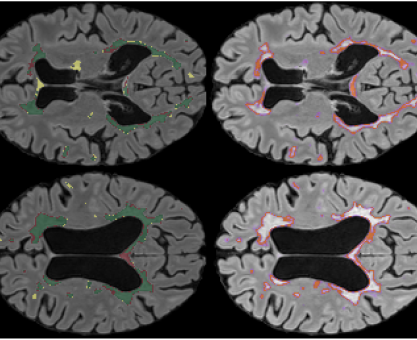
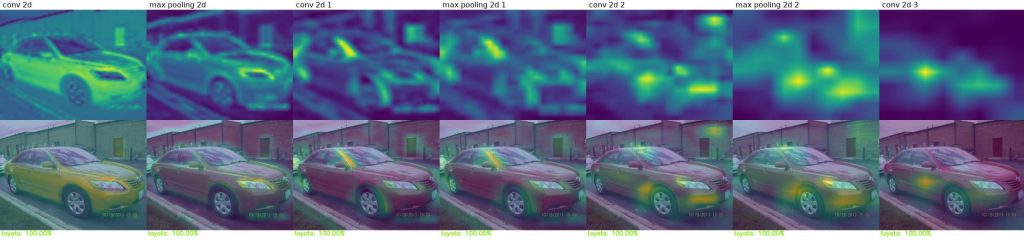
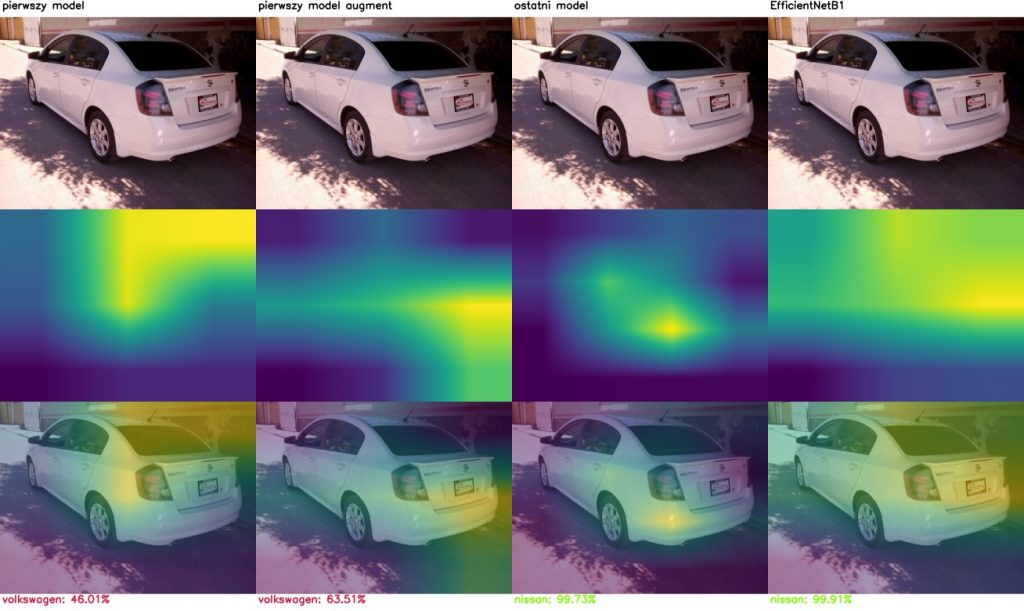
Porównajmy modele pod kątem tego, na podstawie jakich przesłanek podejmują decyzję. Poniżej wyniki CAM (Class activation mapping) dla kolejnych warstw tego samego modelu.
Na zdjęciach ze zbioru treningowego:


A tu na zdjęciach ze zbioru walidacyjnego:
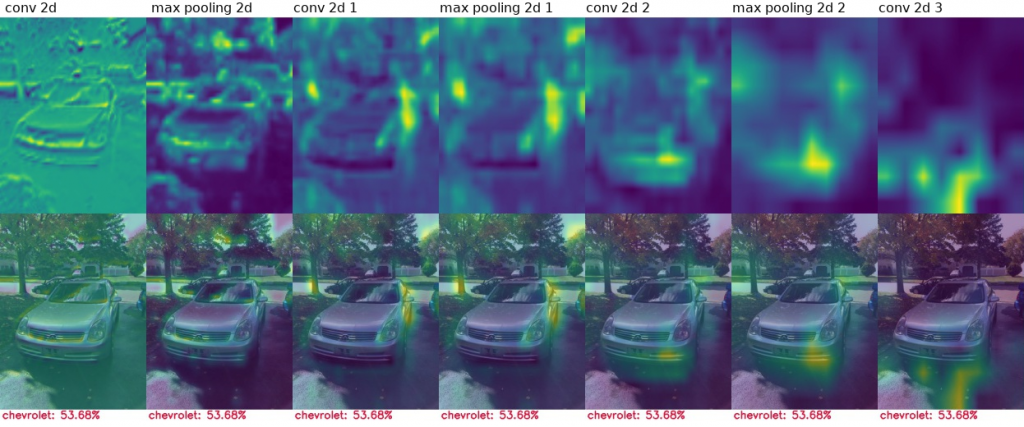


Model generalnie koncentruje się na elementach samochodu, takich jak światła, maskownica lub okolice kół. Czasami błędnie ocenia na podstawie elementów nieistotnych.
Class activation mapping dla wszystkich analizowanych modeli:
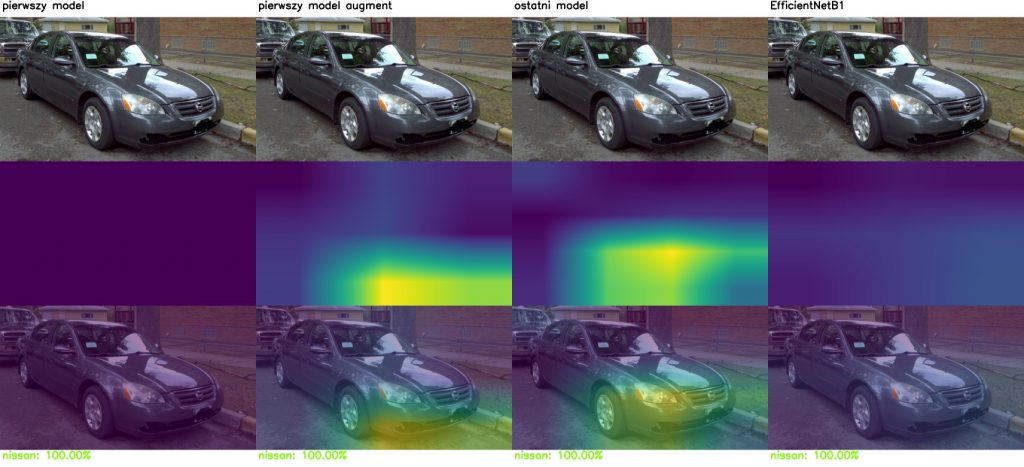
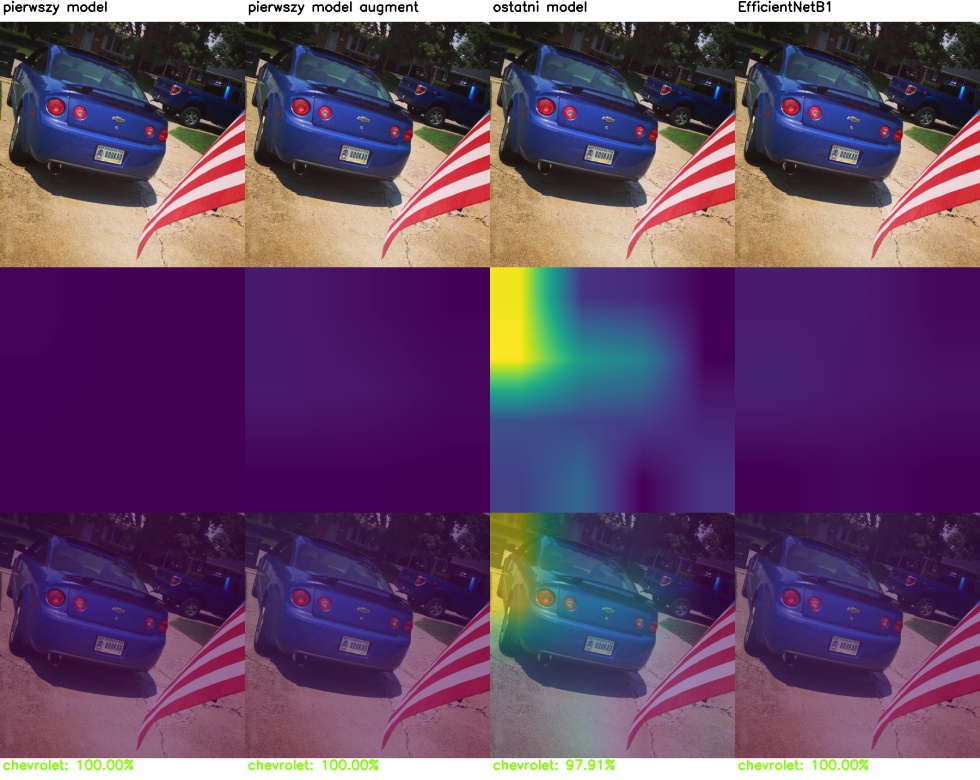
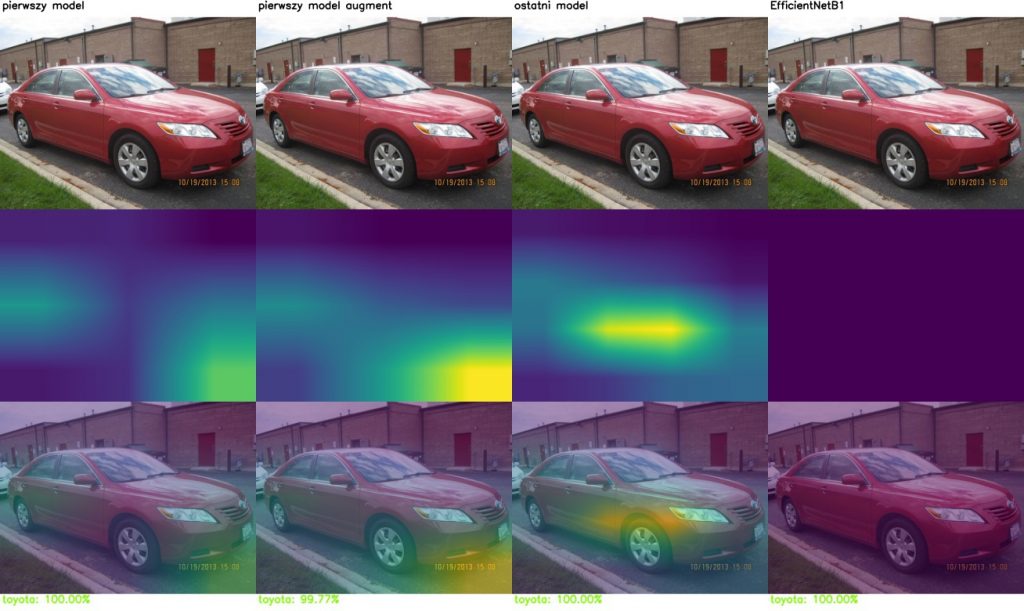
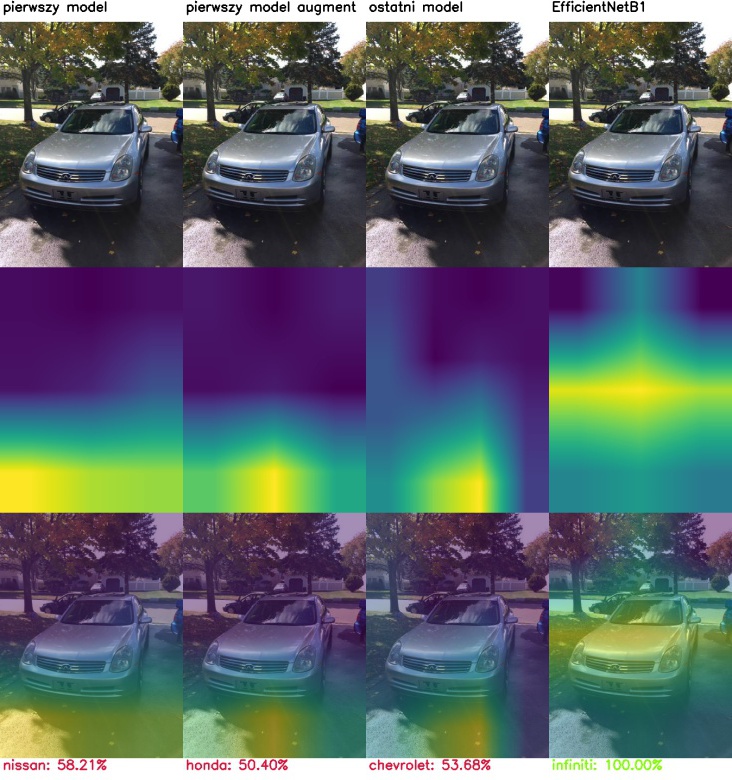
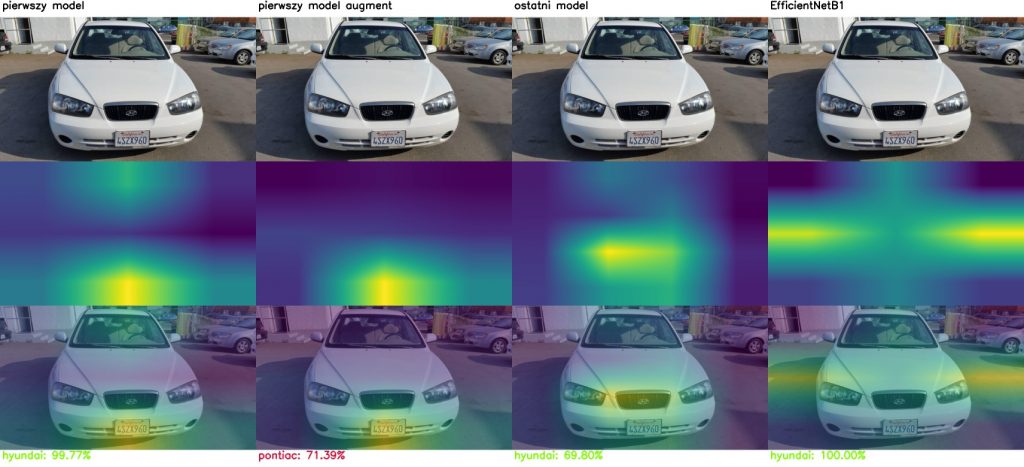
One pixel attack
To technika opublikowana w One pixel attack for fooling deep neural networks mająca na celu zmianę predykcji klasyfikatora po zmianie minimalnej liczby pikseli – najlepiej jednego.
Te testy były rozszerzone na 3 i 5 atakowanych pikseli. Sprawdzanych było 300 losowych zdjęć dla każdego modelu i liczby pikseli.
| liczba atakowanych pikseli | zbiór treningowy success rate | zbiór walidacyjny success rate | |
| pierwszy model bez augmentacji | 1 | 0,05 | 0,31 |
| 3 | 0,29 | 0,51 | |
| 5 | 0,24 | 0,5 | |
| pierwszy model | 1 | 0,07 | 0,17 |
| 3 | 0,27 | 0,39 | |
| 5 | 0,24 | 0,38 | |
| ostatni model | 1 | 0,36 | 0,40 |
| 3 | 0,61 | 0,60 | |
| 5 | 0,60 | 0,59 | |
| model z EfficientNet | 1 | 0,003 | 0,10 |
| 3 | 0,04 | 0,24 | |
| 5 | 0,05 | 0,23 |
Przykładowe udane ataki:



Confusion matrix
Jak wyglądają macierze pomyłek dla 4 modeli?
W ten sposób możemy modele porównać i spróbować odpowiedzieć na pytanie jakiego rodzaju błędy modele robią.
Łatwo zauważyć, że data augmentation zwiększa liczbę pomyłek dla zbioru treningowego – bo trenujemy de facto na nieco innych danych. Natomiast celem data augmentation jest przecież generalizacja, uzyskanie lepszych wyników na zbiorze walidacyjnym i zbiorach testowych, co na szczęście udaje się uzyskać. Zastąpienie własnego, prostego modelu modelem EfficientNet B1 znacząco poprawia wyniki.
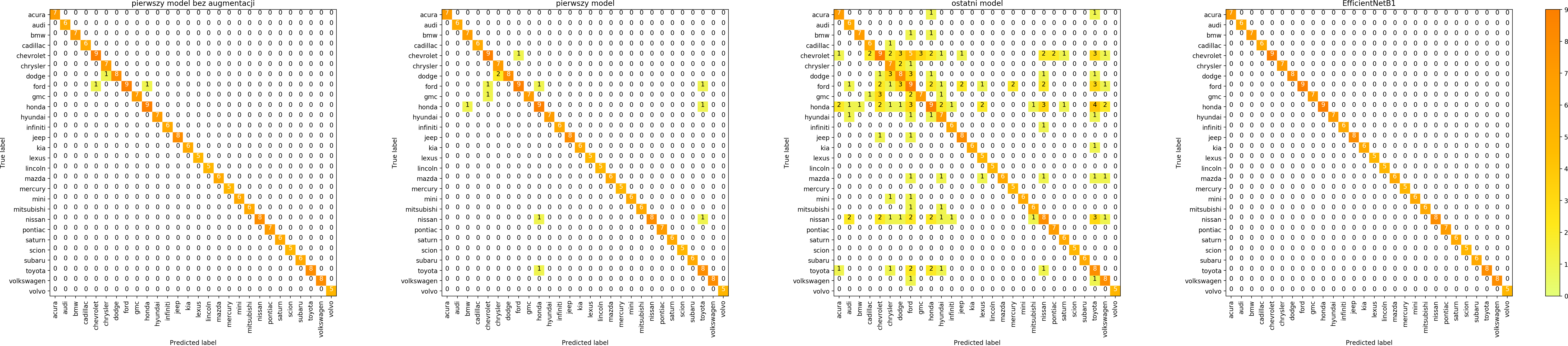
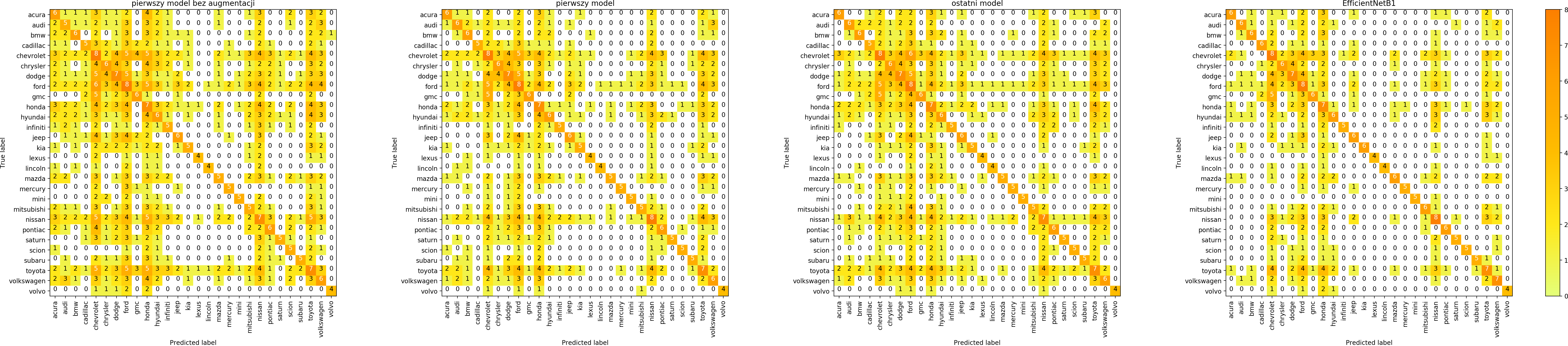
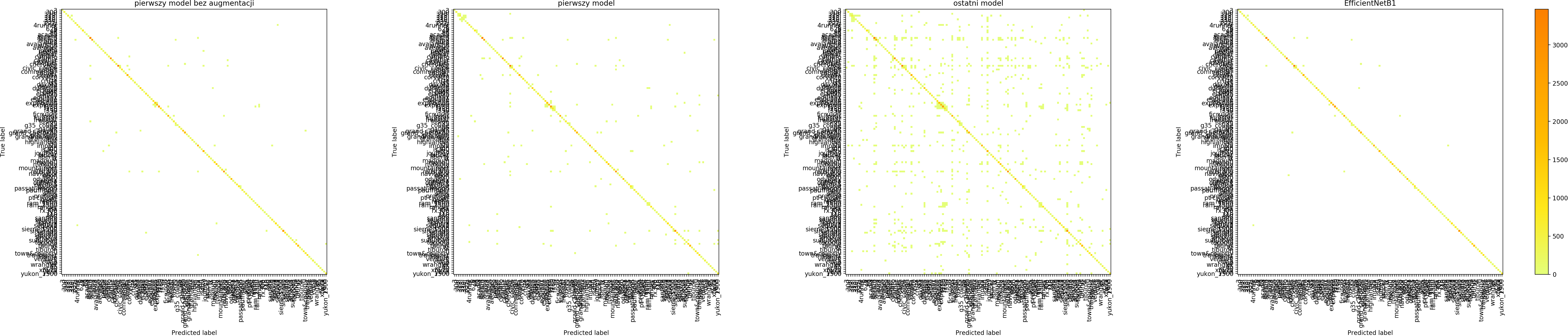

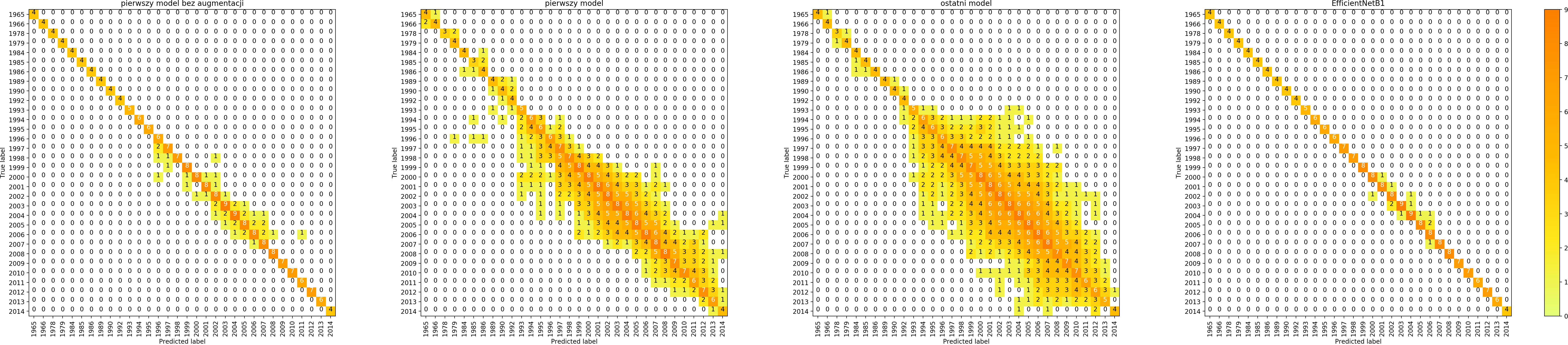
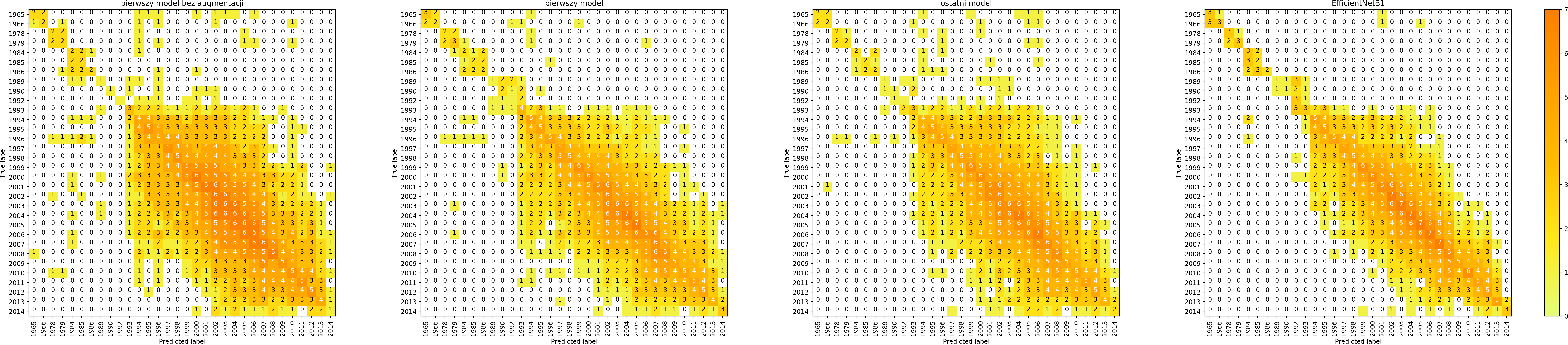
Każdy model potrafił dobrze dostosować się do zbioru treningowego i zdecydowanie gorzej radził sobie ze zbiorem walidacyjnym.
Szczególnie w macierzach dotyczących marki widać, że model chętniej wybiera niektóre klasy – te, których jest więcej w zbiorze treningowym.
Podsumowanie
W poszukiwaniu hiperparametrów do sieci neuronowej lepiej sprawdziła się wiedza teoretyczna niż Optuna.
Model EfficientNet, mimo że ma najmniej parametrów, osiągnął największą dokładność na zbiorze walidacyjnym i był najmniej podatny na zmiany w obrazie (one pixel attack). Tutaj dobrą intuicją jest korzystanie z gotowych architektur State of the art – nie bez powodu te modele miały czas kiedy były najlepsze.
Dla każdego modelu najtrudniejszym zadaniem jest klasyfikacja rocznika, co było możliwe do przewidzenia, ponieważ wewnątrz klas trudno jest znaleźć wspólne cechy.
Co warto byłoby zrobić inaczej?
- zastosować nowsze modele oparte np. na Vision Transformerze (np. SWIN)
- albo EfficientNet v2
- zastosować ordinal regression do predykcji rocznika – bo pomylenie się o rok czy kilka to mniejszy błąd niż pomyłka o kilka dekad (na szczęście takich błedów nie jest dużo)
- HPO – dobór hiperparametrów zwykle pozwala uzyskać lepsze wyniki – kwestia definicji przestrzeni poszukiwań, no i czasu/mocy obliczeniowej.
Linki
Kod do tego posta – https://github.com/deepdrivepl/VMMRdb-simple-CNN
Learning rate warm up: Bag of Tricks for Image Classification with Convolutional Neural Networks in Keras
Optuna: optuna.org
Augmentacja danych: Simple and efficient data augmentations using the Tensorfow tf.Data and Dataset API
Class activation map: Grad-cam: Visualize class activation maps with Keras, TensorFlow and Deep Learning
One pixel attack:
- artykuł: https://arxiv.org/pdf/1710.08864.pdf
- github: https://github.com/Hyperparticle/one-pixel-attack-keras (oficjane repo: https://github.com/Carina02/One-Pixel-Attack w czasie pisania posta niedostępne – czekaliśmy 3 lata już…)
- świetnie opisany notebook na google colab: https://colab.research.google.com/drive/1Zq1kGP9C7i-70-SXyuEEaqYngtyQZMn7
P.S. od Karola: Ten wpis przeczekał lata jako draft, mam nadzieję, że dobrze, że jednak ujrzał światło dzienne. Dodałem tu 2 akapity w 2022 przed publikacją.