Odpowiednio dobrane hiperparametry sieci neuronowej mogą znacznie poprawić jej wyniki, dlatego w tym poście zaprezentuję wykorzystanie różnych narzędzi – Talosa, HParams, Hyperopt i Optuna, które powinny wspomóc nas w tym nieprostym zadaniu. Są to tylko wybrane z licznych, dostępnych możliwości (bardziej dociekliwi mogą poszukać informacji również o np. Spearmint, GPyOpt, SMAC, Autotune, Vizier lub Katib).
Zbiór zawierający zdjęcia samochodów i model konwolucyjnej sieci neuronowej określającej markę, model i rocznik samochodu na podstawie zdjęcia, będą nam służyły za przykład.
Zbiór danych

Baza danych, z której korzystam to Vehicle Make and Model Recognition Dataset (można ją pobrać stąd). Zawiera ona 285’086 zdjęć samochodów, w tym 75 różnych marek, 1’143 modeli i 94 roczników. Ze względu na m.in. obszerność zbioru, wybiorę tylko te klasy (rozumiane jako unikalne marka, model, rocznik), które zawierają co najmniej 100 zdjęć, natomiast pozostałe klasy ograniczę do maksymalnie 200 losowo wybranych zdjęć. Zdjęcia zmniejszyłam do rozmiaru 96×96 i podzieliłam na zbiory treningowy i walidacyjny w proporcji 70:30.
Model
Skorzystam z modelu EfficientNet (GitHub), bez top – tę część zrobię sama i to właśnie do niej będę dobierać hiperparametry.
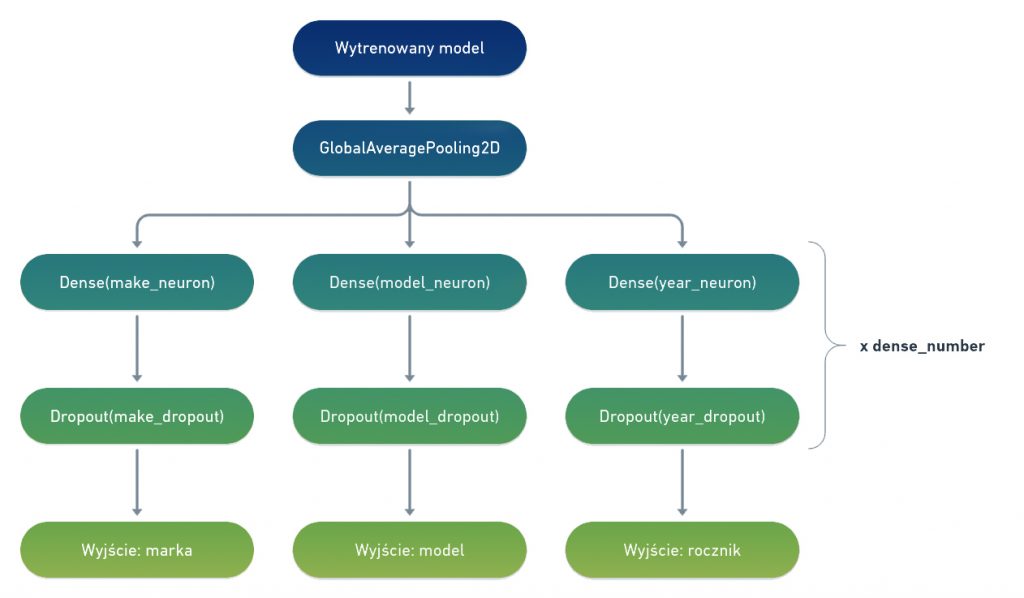
Na schemacie widać 9 parametrów do znalezienia: liczbę warstw dense, liczbę neuronów w każdej z tych warstw i współczynnik dropout dla każdego z wyjść oddzielnie. Ponadto poszukam najlepszej wartości dla regularyzacji L2 i oczywiście prędkości uczenia – learning rate. Jak widać na diagramie – parametry dla marki, modelu i rocznika są niezależne – dlatego będę je wyznaczać oddzielnie, minimalizując loss kolejno dla każdego z wyjść.
Dokładniejszą analizę zbioru i inny model do klasyfikacji można znaleźć w osobnym wpisie.
Model wytrenowałam i zapisałam wagi do części do GlobalAveragePooling. Ta część była wczytywana i zamrażana, żeby uprościć obliczenia.
pre_trained_model = EfficientNetB1(include_top=False,
input_shape=(IMG_WIDTH, IMG_HEIGHT, 3))
pre_trained_model.load_weights('EfficientNetB1_wagi.h5')
for layer in pre_trained_model.layers:
layer.trainable = False
last_output = pre_trained_model.layers[-1].output
x = layers.GlobalAveragePooling2D()(last_output)
Kryteria wyboru
Zanim przejdę do omawiania konkretnych rozwiązań zastanówmy się na co zwrócić uwagę.
Algorytm poszukiwań
Najbardziej znanymi są:
- przeszukiwanie siatki (grid search)
- przeszukiwanie losowe (random search)
- lasy losowe (random forest)
- procesy gaussowskie (Gaussian Processes)
- estymator Parzena (Tree-structured Parzen Estimator)
Linki do artykułów opisujących algorytmy znajdują się w końcowej części postu.
Od skuteczności algorytmu zależy nie tylko, jak dobry model znajdziemy, ale również jak wiele przeliczeń trzeba będzie wykonać.
Pomóc mogą również algorytmy przycinania (ang. pruning algorithm / automated early stopping), które mają wcześniej zakończyć nierokujące próby.
Łatwość użycia
Zastosowanie jakiegokolwiek narzędzia będzie wymagało zmian w kodzie. Warto wiedzieć czy będą one możliwe w naszym modelu.
Podstawy implementacji każdego z narzędzi bez problemu znajdziecie na stronach z dokumentacją.
Wizualizacja
Dobra prezentacja, albo przynajmniej łatwy dostęp do wyników może znacznie ułatwić znalezienie najlepszych hiperparametrów. Chociaż, tak jak w poprzednim przypadku, tutaj też ocena będzie subiektywna.
Dokumentacja
Element szczególnie istotny kiedy poznajemy nowe narzędzie lub napotkamy problem podczas użytkowania. Jeśli zdecydujemy się na popularną bibliotekę łatwiej będzie znaleźć pomoc np. na stack overflow czy githubie.
Talos
Charakterystyka
Talos oferuje 2 metody poszukiwań: przeszukiwanie siatki i przeszukiwanie losowe. Ponadto Talos może automatycznie ograniczać przestrzeń parametrów, korzystając z metod probabilistycznych.
Skorzystałam z przeszukiwania losowego, które zakończyłam po 128 próbach.
Teoretycznie (wg. dokumentacji) Talos powinien działać ze wszystkimi modelami w Kerasie. Wersje Talosa 0.x współpracują z TF 1.15.x i niższymi, natomiast Talos 1.0 z TF 2.0 i wyższymi. Teoretycznie… Ze względu na szybkość przeliczeń dane do modelu podawałam jako tf.data.Dataset, co nie jest wprost obsługiwane przez Talosa.
Talos zapisuje wyniki do pliku .csv po zakończeniu przeliczania każdego modelu, dlatego nawet jeśli poszukiwania zostaną przerwane – nie stracimy wyników. Jednak po ponownym uruchomieniu treningu nie będzie wiedział, jakie kombinacje parametrów zostały już przeliczone. Plik .csv w pierwszym wierszu zawiera nazwy parametrów i metryk modelu, dlatego jeśli zmienimy parametry lub metryki to porównanie modeli będzie od nas wymagało dodatkowego przekształcania danych.
Dokumentacja z kodem i przykładami jest dostępna tutaj: GitHub , a prosty opis i instrukcja uruchamiania tutaj: Docs (ładnie przedstawione, niestety nieaktualne i niepełne).
Pseudo kod
hyperparam = {
'num_dense_make': [1,2,3,4,5,6,7,8,9,10,11,12,13,14],
'num_dense_model': [1,2,3,4,5,6,7,8,9,10,11,12,13,14],
'num_dense_year': [1,2,3,4,5,6,7,8,9,10,11,12,13,14],
'make_neuron': [64, 128, 256, 512, 1024, 2048],
'model_neuron': [64, 128, 256, 512, 1024, 2048],
'year_neuron': [64, 128, 256, 512, 1024, 2048],
'make_dropout': [0,0.05,0.1,0.15,0.2,0.25,0.3,0.35,0.4,0.45,0.5],
'model_dropout': [0,0.05,0.1,0.15,0.2,0.25,0.3,0.35,0.4,0.45,0.5],
'year_dropout': [0,0.05,0.1,0.15,0.2,0.25,0.3,0.35,0.4,0.45,0.5],
'learning_rate': [0.0000001,0.0000003,0.000001,0.000003,0.00001,0.00003,0.0001,0.0003,0.001,0.003,0.01,0.03,0.1],
'L2': [0.0000001,0.0000003,0.000001,0.000003,0.00001,0.00003,0.0001,0.0003,0.001,0.003,0.01]
}
mirrored_strategy = tf.distribute.MirroredStrategy()
def params_search(x, y, x_val, y_val, hparams):
with mirrored_strategy.scope():
# wczytanie modelu EfficientNet
l2 = tf.keras.regularizers.l2(hparams['L2'])
x = layers.GlobalAveragePooling2D()(last_output)
l_make = layers.Dense(hparams['make_neuron'], activation='relu', kernel_regularizer = l2)(x)
l_model = layers.Dense(hparams['model_neuron'], activation='relu', kernel_regularizer = l2)(x)
l_year = layers.Dense(hparams['year_neuron'], activation='relu', kernel_regularizer = l2)(x)
for i in range(int(hparams['num_dense_make']-1)):
l_make = layers.Dense(hparams['make_neuron'], activation='relu', kernel_regularizer = l2)(l_make)
l_make = layers.Dropout(hparams['make_dropout'])(l_make)
for i in range(int(hparams['num_dense_model']-1)):
l_model = layers.Dense(hparams['model_neuron'], activation='relu', kernel_regularizer = l2)(l_model)
l_model = layers.Dropout(hparams['model_dropout'])(l_model)
for i in range(int(hparams['num_dense_year']-1)):
l_year = layers.Dense(hparams['year_neuron'], activation='relu', kernel_regularizer = l2)(l_year)
l_year = layers.Dropout(hparams['year_dropout'])(l_year)
output_make = layers.Dense(len(CLASS_NAMES_MAKE), activation='softmax', name='output_make')(l_make)
output_model = layers.Dense(len(CLASS_NAMES_MODEL), activation='softmax', name='output_model')(l_model)
output_year = layers.Dense(len(CLASS_NAMES_YEAR), activation='softmax', name='output_year')(l_year)
cnn = keras.Model(inputs=pre_trained_model.input, outputs=[output_make, output_model, output_year], name='cars_model')
cnn.compile(optimizer='Adam', loss='categorical_crossentropy',
loss_weights=[1., 1., 1.], metrics=['acc'])
early_stop = keras.callbacks.EarlyStopping(monitor='val_loss', patience=20, verbose=1, restore_best_weights=True)
#LR warmup callback
out = cnn.fit(train_set, steps_per_epoch = STEPS_PER_EPOCH_TRAIN,
epochs = 100, callbacks=[early_stop, warm_up_lr],
validation_data = test_set, validation_steps = STEPS_PER_EPOCH_VAL)
return out, cnn
# talosowi podaję te same dane, ale w postaci np.array, ponieważ tf.data nie jest obsługiwane
t = talos.Scan(x=X_train,
y=[Y_train_make, Y_train_model, Y_train_year],
x_val=X_test,
y_val=[Y_test_make, Y_test_model, Y_test_year],
params=hyperparam,
model=params_search,
experiment_name='talos',
fraction_limit=.000000001,
random_method='quantum')
Działanie
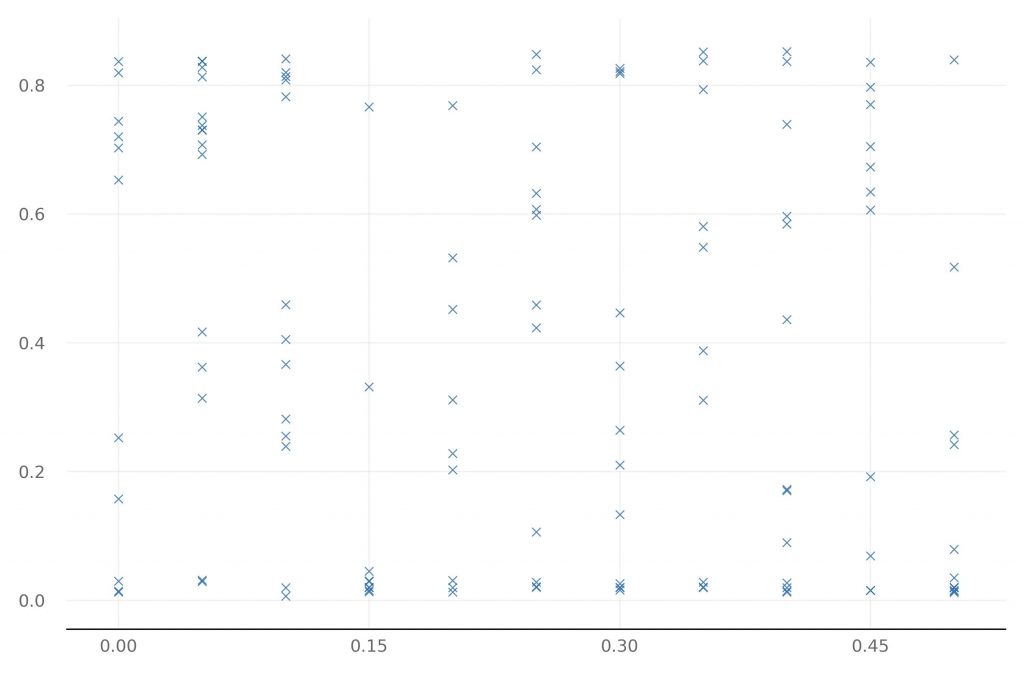
Jak wcześniej wspomniałam, Talos przeliczył 128 modeli. Korzystając z jego narzędzi do wizualizacji, możemy obejrzeć wyniki:
import talos
ao = talos.Analyze('wyniki.csv')
ao.plot_bars('num_dense_model', 'val_output_model_acc',
'model_dropout', 'model_neuron')
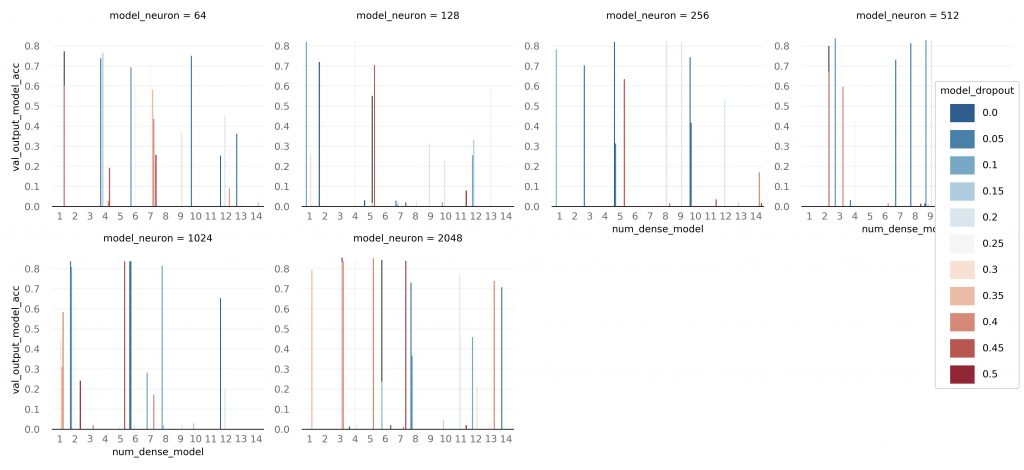
ao.plot_regs('num_dense_model', 'val_output_model_acc')
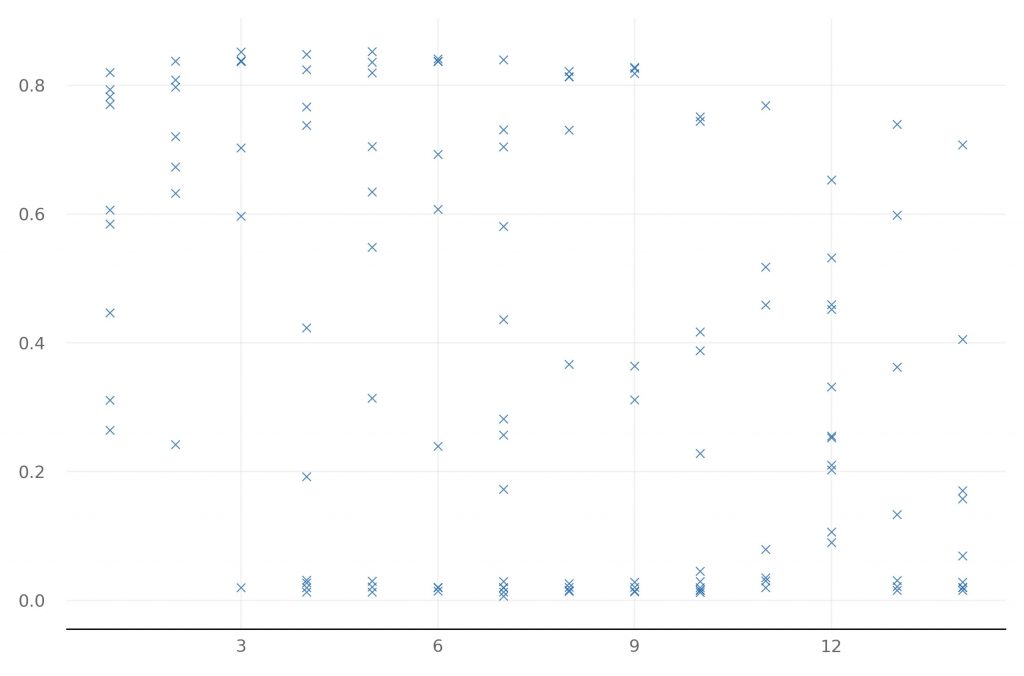
ao.plot_regs('model_neuron', 'val_output_model_acc')
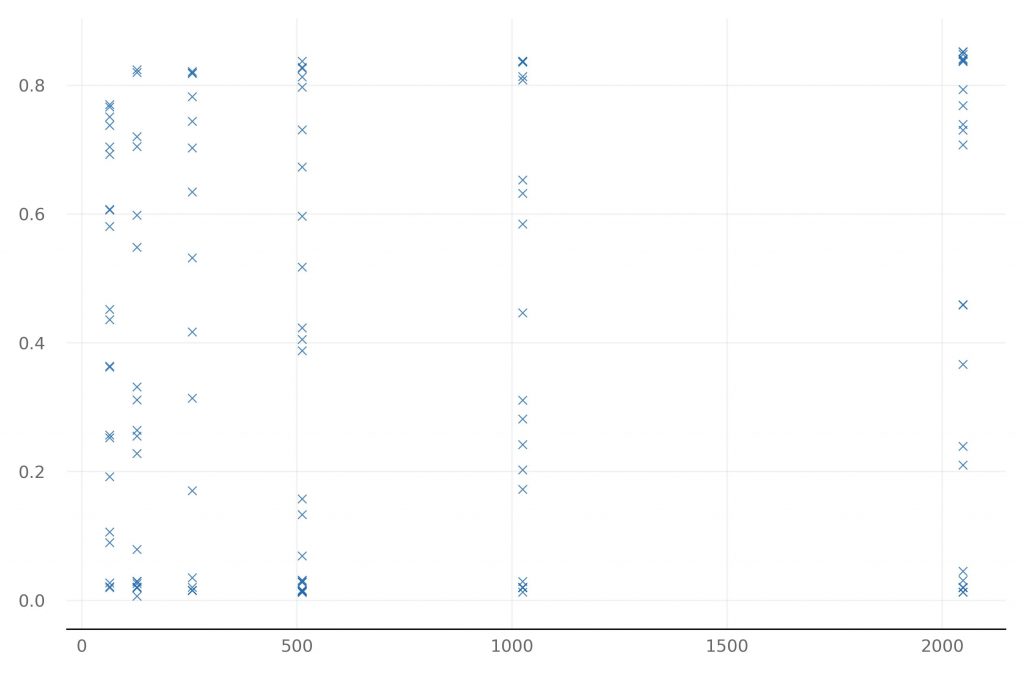
ao.plot_regs('model_dropout', 'val_output_model_acc')
HParams
HParams nie służy do przeszukiwania przestrzeni parametrów, a tylko (i aż) do wizualizacji. W połączeniu z Kerasem jest prosty w implementacji – wystarczy dodać jeden callback i hiperparametry razem z metrykami mamy zapisywane i prezentowane w tabelce i na wykresach (poniżej).
Dokumentacja dostępna jest tu: Tensorflow.org
Jedynym problemem, który tu napotkałam było to, że chociaż HParams uruchamia się w Tensorboard 1.15, do prawidłowego działania potrzebowałam Tensorboard 2.0.
Ponieważ HParams służy do wizualizacji, natomiast w Hyperopt wizualizacji (prawie) nie ma, z tych dwóch narzędzi będę korzystała jednocześnie.
Hyperopt
Charakterystyka
Hyperopt udostępnia 3 algorytmy poszukiwań: przeszukiwanie losowe, estymator Parzena i adaptacyjny estymator Parzena. Skorzystałam z estymatora Parzena z ustawieniami domyślnymi.
Hyperopt jest niezależny od funkcji, którą optymalizuje – to znaczy wystarczy, że będzie ona zwracała wartość, która ma być minimalizowana lub maksymalizowana – nie miałam więc żadnych problemów w połączeniu modelu z Hyperopt (i z HParams).
Jednocześnie pozwala na tworzenie parametrów zagnieżdżonych, dzięki czemu (w razie potrzeby) można tworzyć złożone przestrzenie parametrów.
Wizualizacja i dokumentacja są zdecydowanie słabymi punktami Hyperopt. Do wizualizacji są dostępne 3 funkcje (poniżej).
Dokumentacja, kod i przykłady znajdują się tutaj: GitHub i tu: Docs. Ponadto w internecie znajdziecie wiele przykładów zastosowań.
Pseudo kod
hyperparam = { 'num_dense_make': hpo.quniform('num_dense_make', 1, 14, 1),
'make_neuron': hpo.choice('make_neuron', [64, 128, 256, 512, 1024, 2048]),
'make_dropout': hpo.quniform('make_dropout', 0, 0.5, 0.05),
'learning_rate': hpo.loguniform('learning_rate', -16.1, -2.3),
'L2': hpo.loguniform('L2', -16.1, -4.6) }
mirrored_strategy = tf.distribute.MirroredStrategy()
def params_search(hparams):
with mirrored_strategy.scope():
#wczytanie modelu EfficientNet
l_make = layers.Dense(hparams['make_neuron'], activation='relu', kernel_regularizer = l2)(x)
for i in range(int(hparams['num_dense_make']-1)):
l_make = layers.Dense(hparams['make_neuron'], activation='relu', kernel_regularizer = l2)(l_make)
l_make = layers.Dropout(hparams['make_dropout'])(l_make)
output_make = layers.Dense(len(CLASS_NAMES_MAKE), activation='softmax', name='output_make')(l_make)
cnn = keras.Model(inputs=pre_trained_model.input, outputs=output_make)
cnn.compile(optimizer='Adam', loss='categorical_crossentropy', metrics=['acc'])
early_stop = keras.callbacks.EarlyStopping(monitor='val_loss', patience=30, verbose=1, restore_best_weights=True)
logdir = 'logdir'
tbcall = tf.keras.callbacks.TensorBoard(logdir, profile_batch=0)
hpcall = hp.KerasCallback(logdir, hparams)
#LR warmup callback
cnn.fit(train_set, steps_per_epoch = STEPS_PER_EPOCH_TRAIN,
epochs = 100, callbacks=[tbcall, hpcall, early_stop, warm_up_lr],
validation_data = test_set, validation_steps = STEPS_PER_EPOCH_VAL)
loss, make_acc = cnn.evaluate(test_set, steps=STEPS_PER_EPOCH_VAL)
return loss
tpe_algo = tpe.suggest
tpe_trials = Trials()
tpe_best = fmin(fn=params_search, space=hyperparam,
algo=tpe_algo, trials=tpe_trials,
max_evals=100)
joblib.dump(tpe_trials, 'make.pkl') #jeśli chcemy zapisać wyniki
Działanie
Hyperopt przeliczył w sumie 300 modeli (po 100 dla każdego z wyjść, w tym pierwszych 20 było losowych). Za pomocą hyperopt.plotting możemy wyświetlić wykresy:
from hyperopt import plotting
trials = joblib.load('make.pkl')
plotting.main_plot_history(trials)
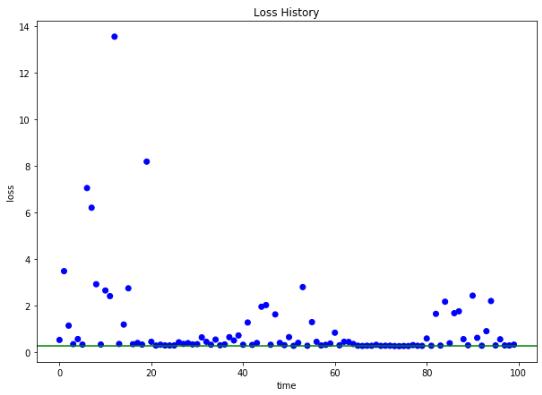
plotting.main_plot_histogram(trials)
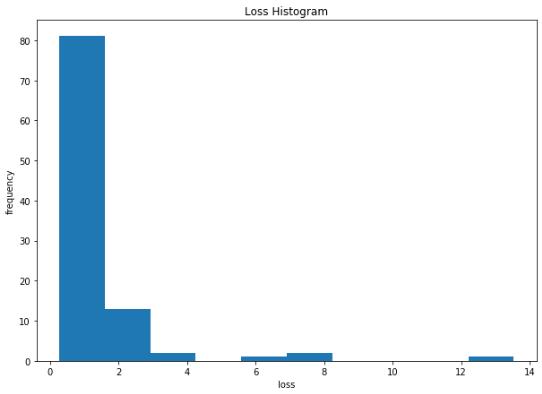
plotting.main_plot_vars(trials)
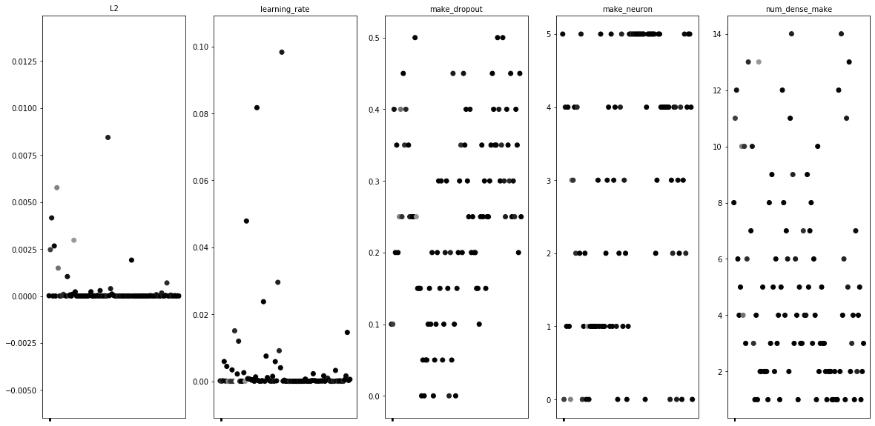
Są to wykresy tylko dla jednego z wyjść. Jak widać – bardzo brakuje tu jakiejkolwiek możliwości modyfikacji – chociażby skali logarytmicznej dla L2 i learning rate, ponadto oś przy „make_neuron” w ostatnim wykresie jest źle podpisana. Przejdę więc od razu do analizy wyników Hyperopt korzystając z HParams.
Działanie Hyperopt – wizualizacja HParams
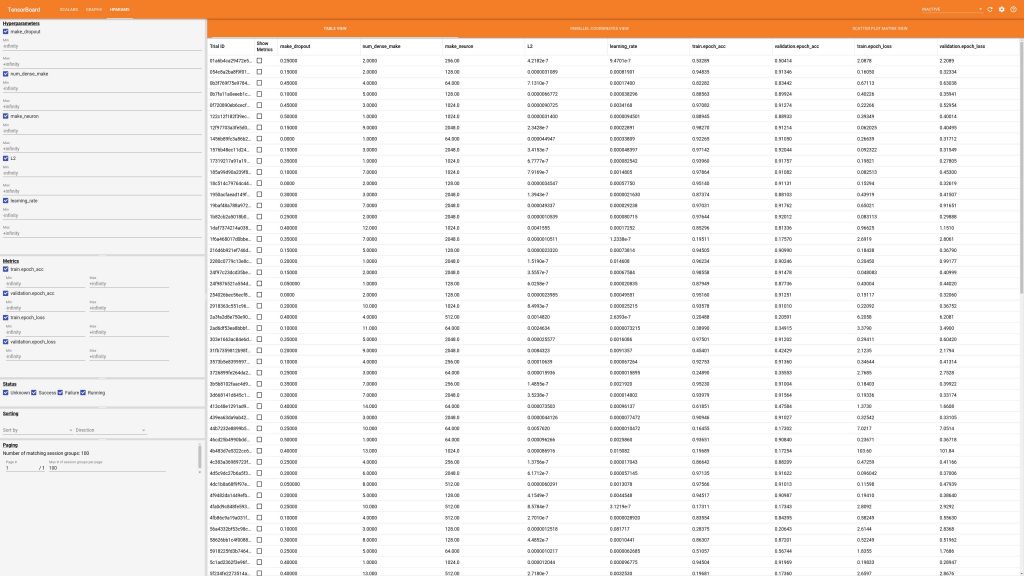
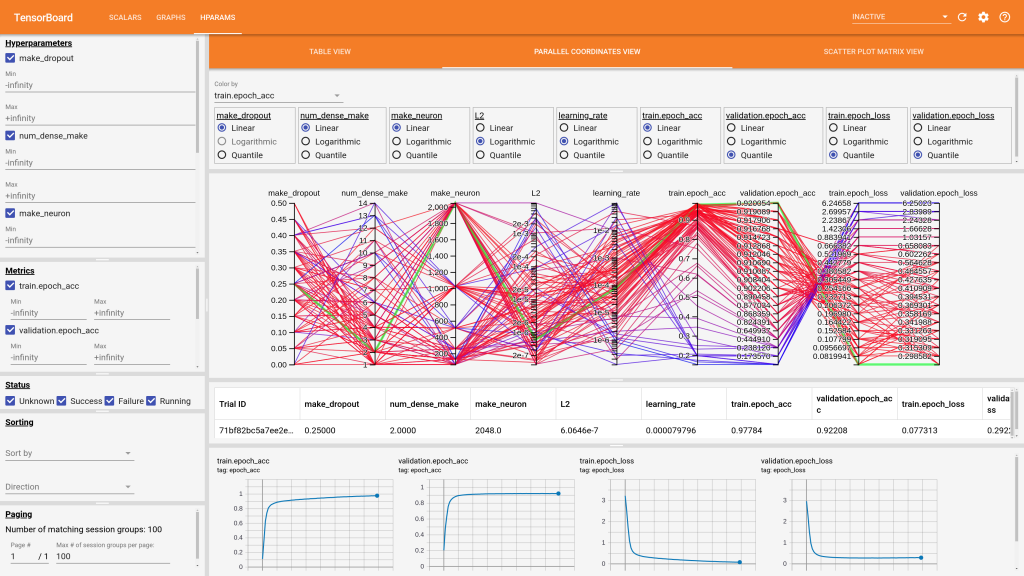
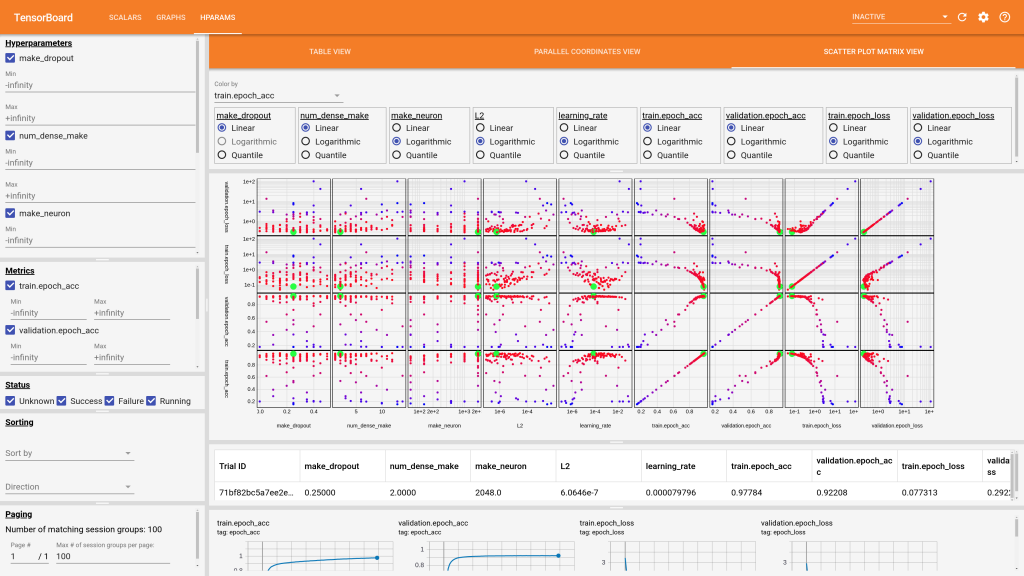
Dodatkowe uwagi: rozdzielczość 1600×900 często nie jest wystarczająca do wyświetlania wyników z HParams. Screenshoty zostały dodatkowo wygenerowane w 4K i to jest niezły wybór do wyświetlania wykresów. Jeśli mamy dane o wielu różnych hiperparametrach, parallel coordinates view będzie trudny do używania – wykres rozsunie się daleko poza granice ekranu.
Optuna
Charakterystyka
Optuna oferuje te same algorytmy co Hyperopt, czyli przeszukiwanie losowe i estymator Parzena. Ponownie wybrałam estymator Parzena. Jednak dodatkowo w Optunie możemy automatycznie „przycinać” nierokujące próby metodą ASHA (Asynchronous Successive Halving) i to również wykorzystam.
Stosując nazewnictwo twórców: Optuna stosuje zasadę define-by-run (w przeciwieństwie do define-and-run), czyli parametry do danej próby są dobierane w trakcie jej trwania (w przeciwieństwie do wybierania parametrów przed rozpoczęciem próby). Oznacza to, że przy bardziej skomplikowanych zadaniach nie trzeba tworzyć złożonej struktury parametrów, a kod może być bardziej czytelny. Ze względu na to pozwolę, żeby Optuna dobierał liczbę neuronów dla każdej warstwy osobno – przez co znacznie wzrośnie liczba parametrów, ale być może uda się znaleźć lepsze rozwiązanie.
Wizualizacja w Optuna przypomina tę z TensorBoard. Do dyspozycji mamy gotowe wykresy, jednak dane możemy łatwo przekazać do pandasowej DataFrame, więc możemy je zaprezentować również na inne sposoby. Wykresy poniżej.
Dokumentacja – wg. mnie Optuna jest najlepiej opisanym narzędziem z prezentowanych tutaj. Dostępna jest strona internetowa, tutorial i repozytorium na GitHub.
Pseudo kod
def params_search(trial):
with mirrored_strategy.scope():
# wczytanie modelu EfficientNet
l_dwa = trial.suggest_loguniform('l_2', 1e-7, 1e-2)
l2 = tf.keras.regularizers.l2(l_dwa)
x = layers.GlobalAveragePooling2D()(last_output)
num_dense_make = trial.suggest_int('num_dense_make', 1, 14)
make_neuron = trial.suggest_loguniform('make_neuron_1', 64, 2048)
make_dropout = trial.suggest_discrete_uniform('make_dropout_1', 0.0, 0.5, 0.05)
l_make = layers.Dense(make_neuron, activation='relu', kernel_regularizer = l2)(x)
for i in range(int(num_dense_make-1)):
make_neuron = trial.suggest_loguniform('make_neuron_{}'.format(i+2), 64, 2048)
l_make = layers.Dense(make_neuron, activation='relu', kernel_regularizer = l2)(l_make)
make_dropout = trial.suggest_discrete_uniform('make_dropout_{}'.format(i+2), 0.0, 0.5, 0.05)
l_make = layers.Dropout(make_dropout)(l_make)
output_make = layers.Dense(len(CLASS_NAMES_MAKE), activation='softmax', name='output_make')(l_make)
cnn = keras.Model(inputs=pre_trained_model.input, outputs=output_make)
cnn.compile(optimizer='Adam', loss='categorical_crossentropy', metrics=['acc'])
learning_rate = trial.suggest_loguniform('learning_rate', 1e-7, 1e-1)
prunning = optuna.integration.TFKerasPruningCallback(trial, 'val_loss')
#LR warmup callback
cnn.fit(train_set, steps_per_epoch = STEPS_PER_EPOCH_TRAIN,
epochs = 100, callbacks=[warm_up_lr, prunning],
validation_data = test_set, validation_steps = STEPS_PER_EPOCH_VAL)
loss, acc = cnn.evaluate(test_set, steps=STEPS_PER_EPOCH_VAL)
return loss
study = optuna.create_study(sampler = TPESampler(n_startup_trials=40))
study.optimize(params_search, n_trials=110)
joblib.dump(study, 'make.pkl') # jeśli chcemy zapisać wyniki
Działanie
Optuna przeliczył w sumie 330 sieci, po 110 dla każdego z wyjść, w tym 40 pierwszych było losowych (domyślnie jest to 10). Optuna skróciła 75 testów dla marki, 82 dla modelu i 84 dla rocznika, co znacznie przyspieszyło obliczenia.
from optuna.visualization import plot_contour, plot_optimization_history, plot_parallel_coordinate, plot_slice
import joblib
study = joblib.load('wyniki.pkl')
plot_contour(study, params=['learning_rate',
'make_neuron_1',
'num_dense_make'])
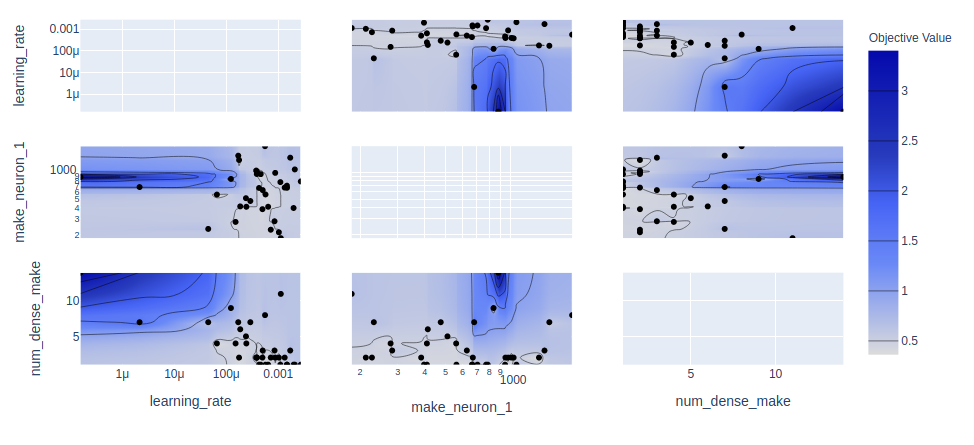
plot_parallel_coordinate(study, params=['l_1',
'learning_rate',
'make_neuron_1',
'num_dense_make'])
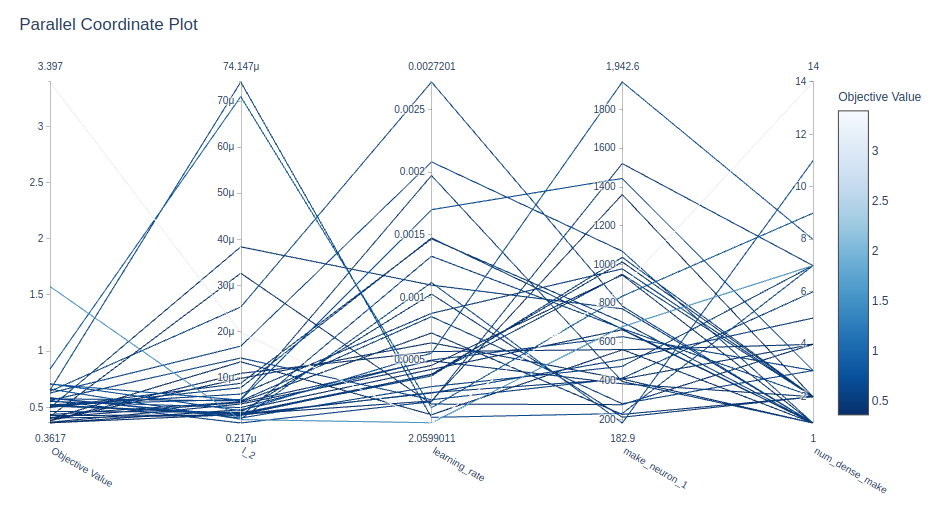
plot_slice(study, params=['learning_rate', 'make_neuron_1'])
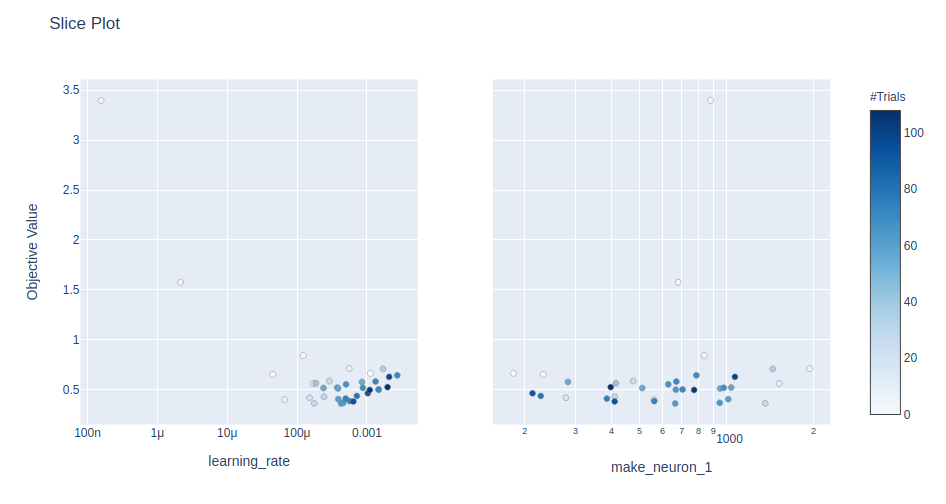
Uwagi: Optuna w wykresach uwzględnia tylko próby, ze statusem Complete, te ze statusem Pruned nie są widoczne. Przy testach zdarzyło się, że najlepszy wynik nie był widoczny, dlatego wg. mnie, lepiej spojrzeć na wyniki (np. przekazując je do DataFrame). Dla ułatwienia:
df = study.trials_dataframe(attrs=('number', 'value', 'params', 'state'))
Porównanie wyników
Po zakończeniu testów przeliczyłam jeszcze każdą z sieci z odmrożonymi warstwami z EfficientNet, czego skutkiem było zmniejszenie dokładności klasyfikacji marki i modelu, ale jednocześnie zwiększenie dokładności klasyfikacji roczników. W celu poprawienia działania sieci należałoby jeszcze np. dodać augmentację danych, ponieważ sieci wyraźnie się przetrenowywały, ale o tym już w kolejnym poście.
| Talos | Hyperopt | Optuna | |
| Liczba przeliczonych modeli | 128 | (100, 100, 100)* | (110, 110, 110)* |
| Po ilu przeliczeniach znaleziono najlepsze parametry* | 73, 43, 11* | 75, 92, 25* | 64, 66, 3* |
| Otrzymana dokładność klasyfikacji (zamrożony EfficientNet): | |||
| marek [%] | 92,0 | 91,8 | 91,9 |
| modeli [%] | 85,2 | 81,4 | 84,4 |
| roczników [%] | 36,6 | 18,3 | 35,2 |
| Dokładność klasyfikacji po odmrożeniu części EfficientNet: | |||
| marek [%] | 83,47 | 87,22 | 87,33 |
| modeli [%] | 78,57 | 81,34 | 81,24 |
| roczników [%] | 33,93 | 31,65 | 37,01 |
* odpowiednio dla marki, modelu i rocznika
Wizualizacje wyników
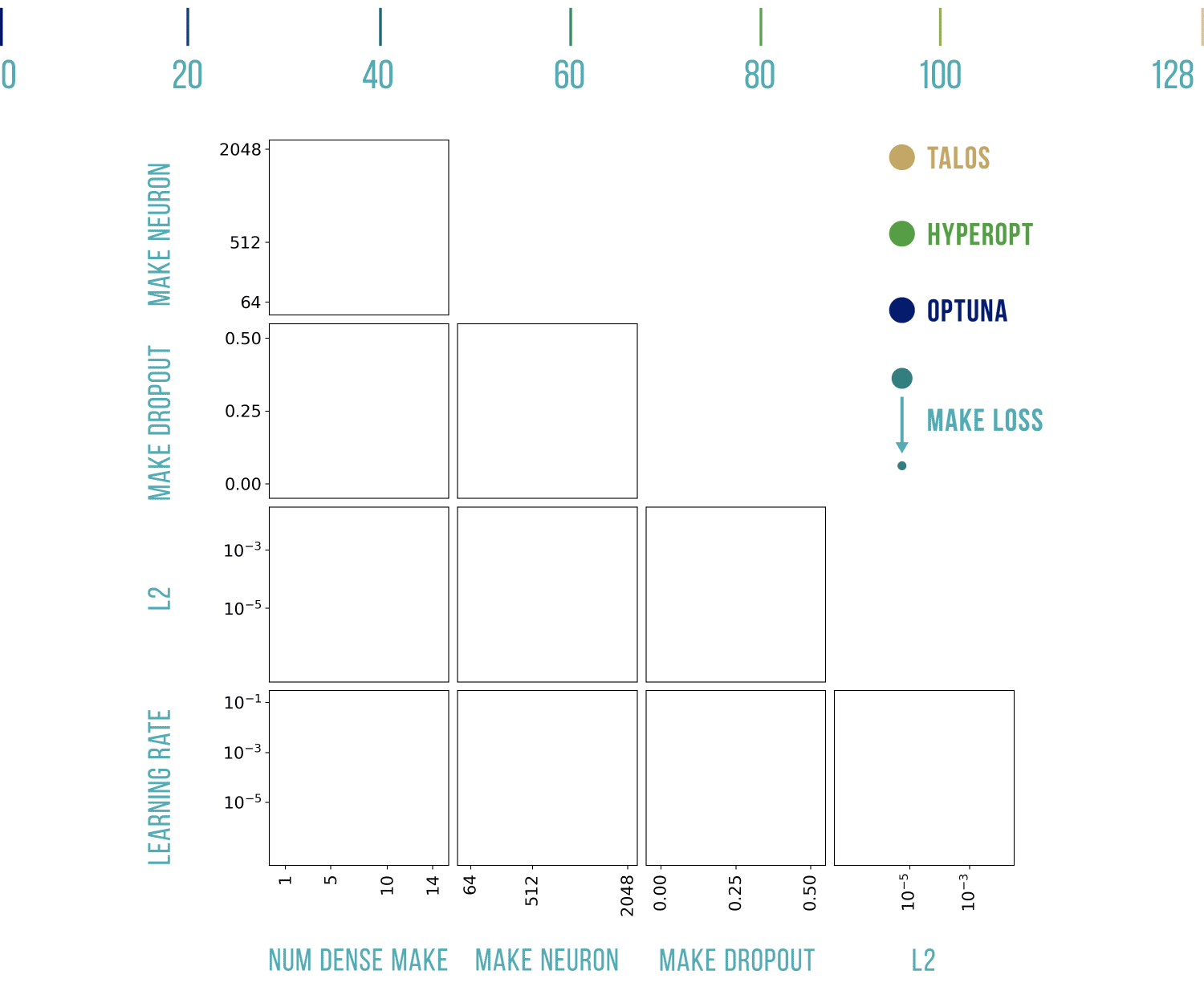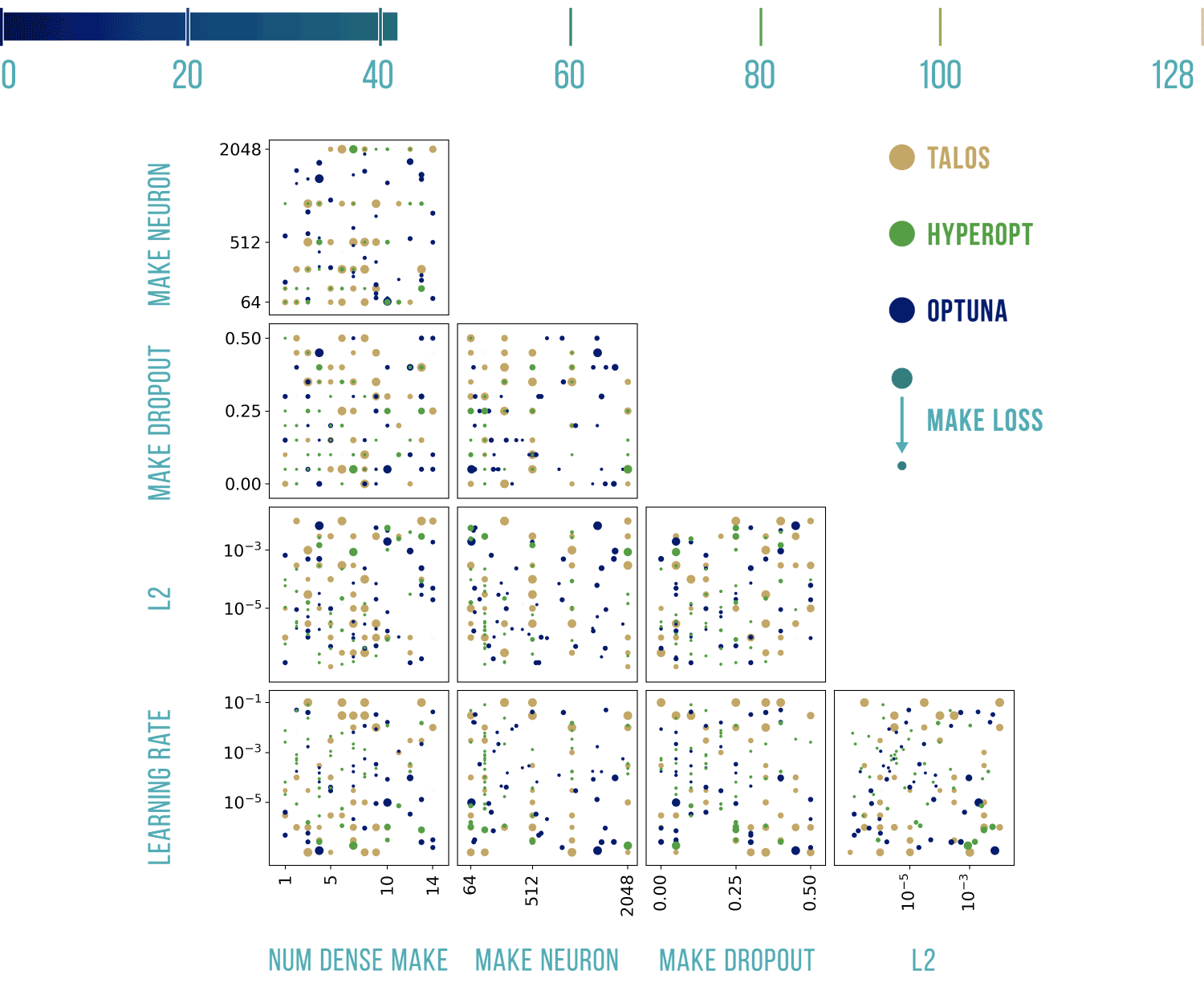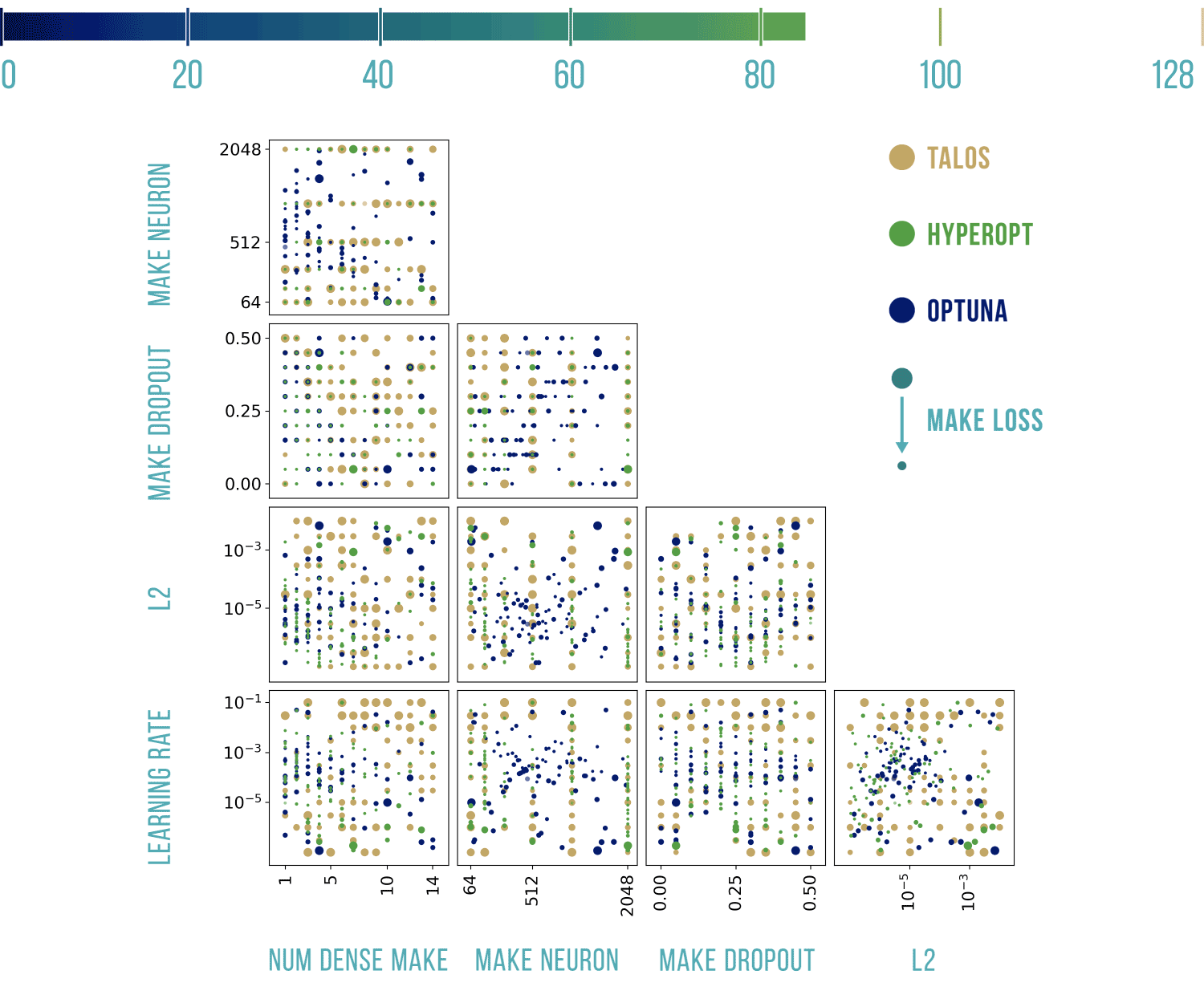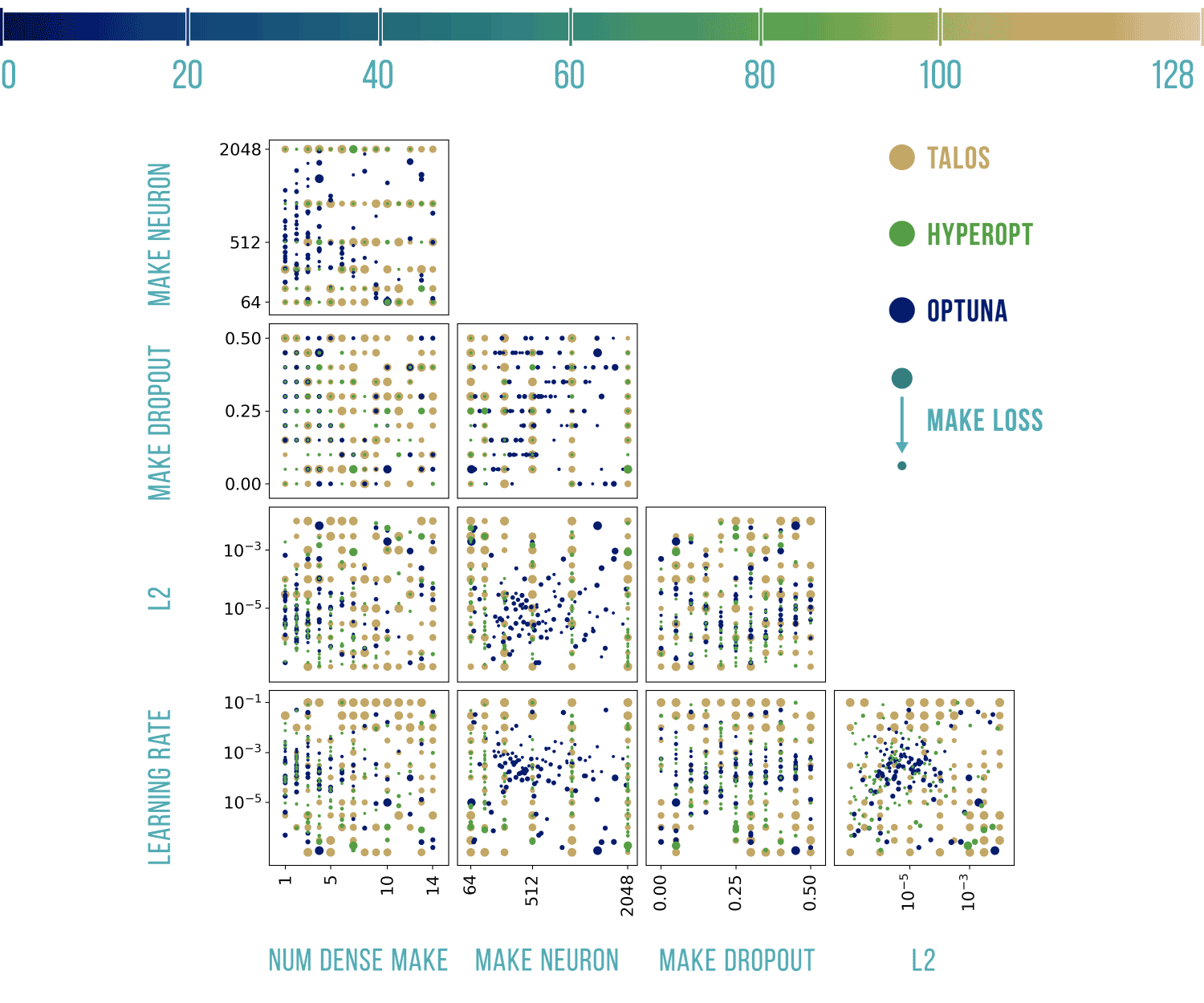
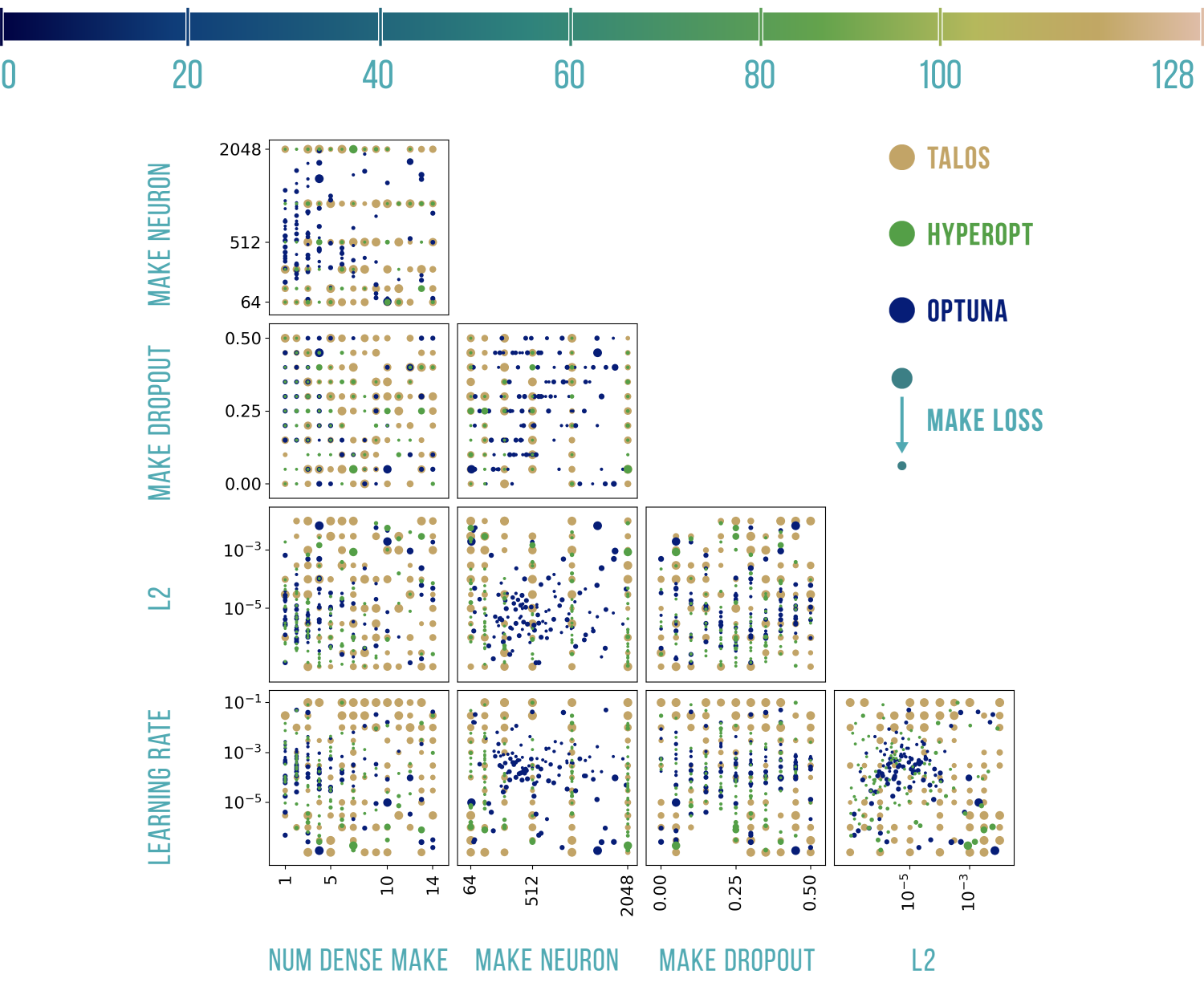
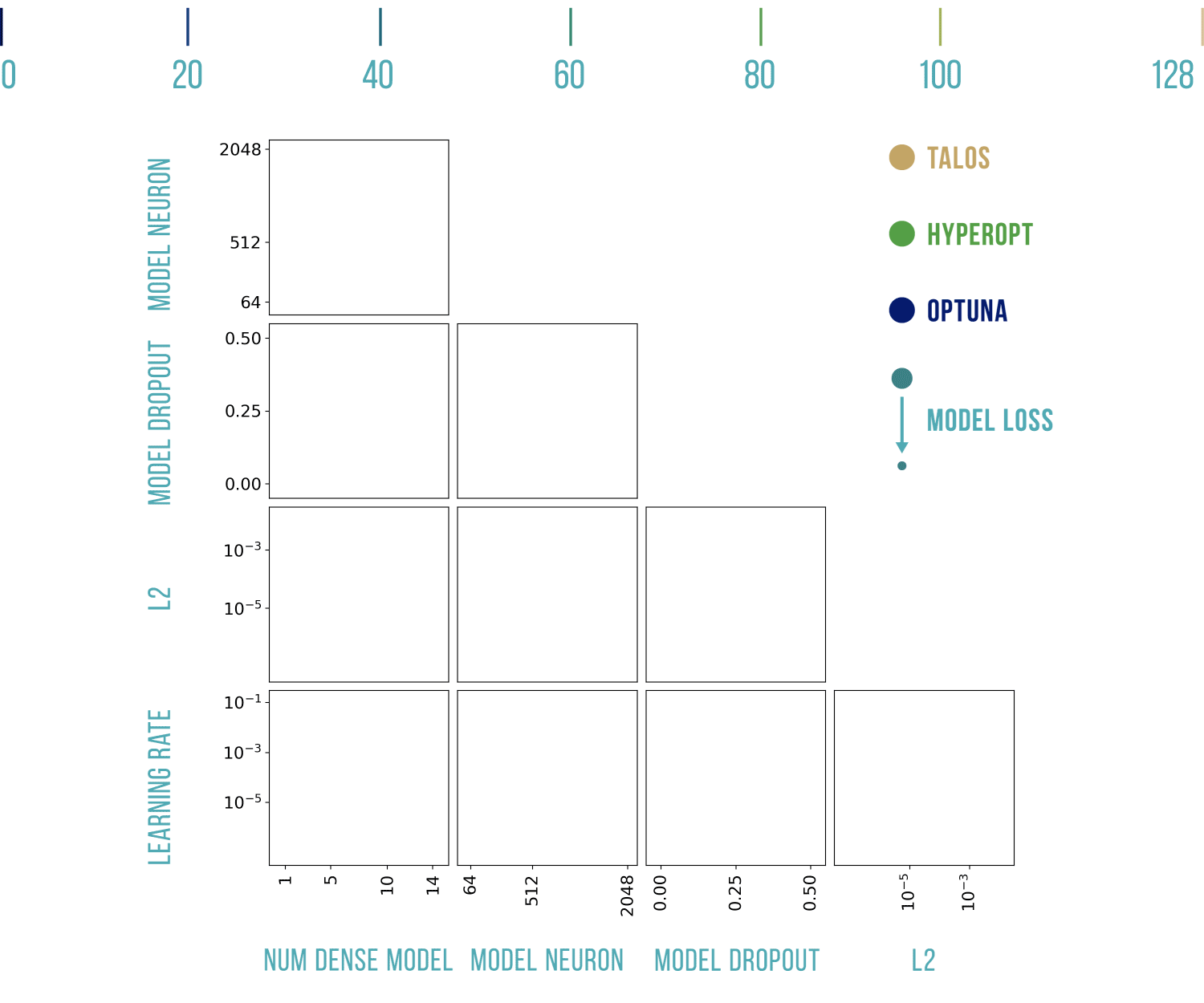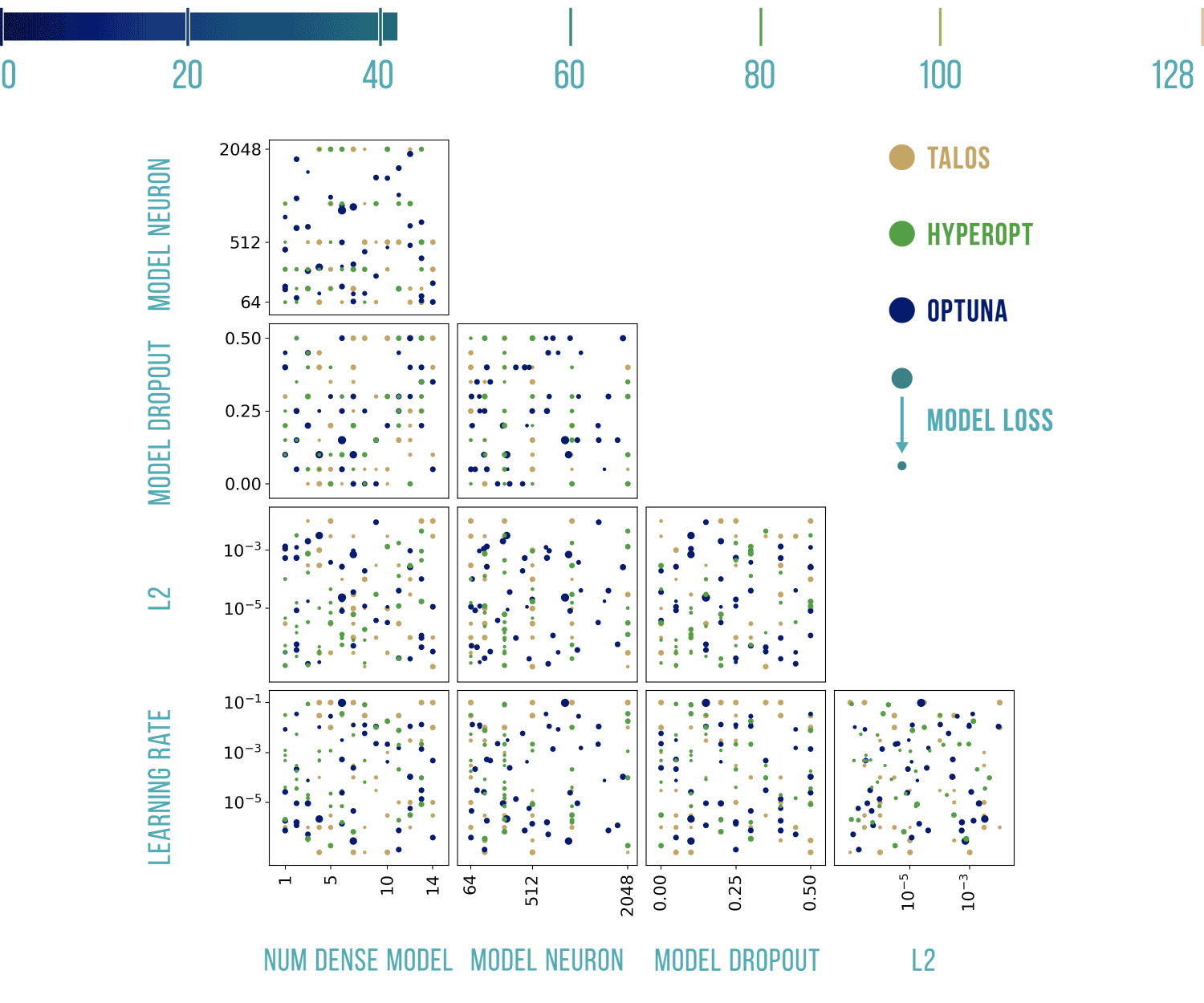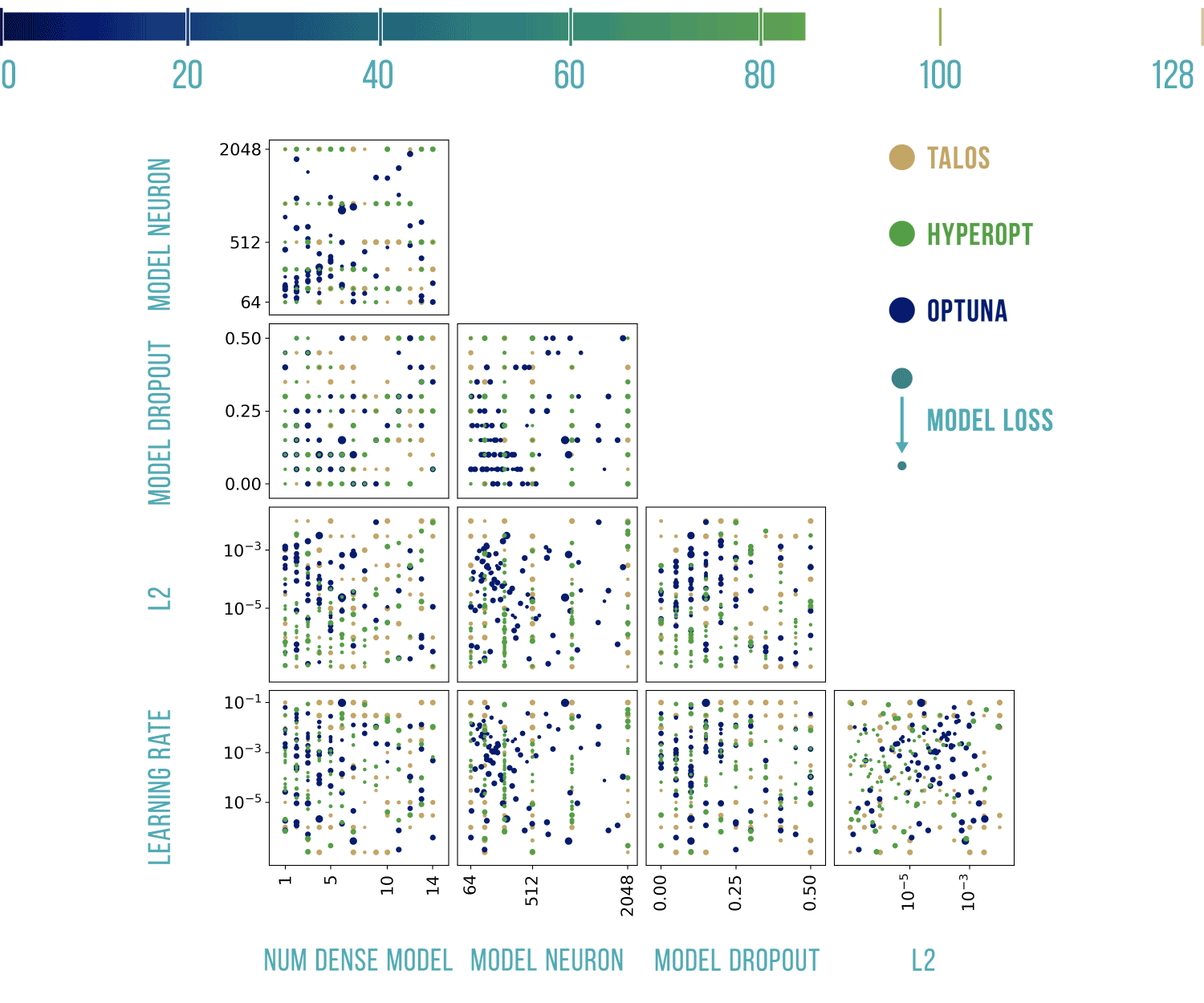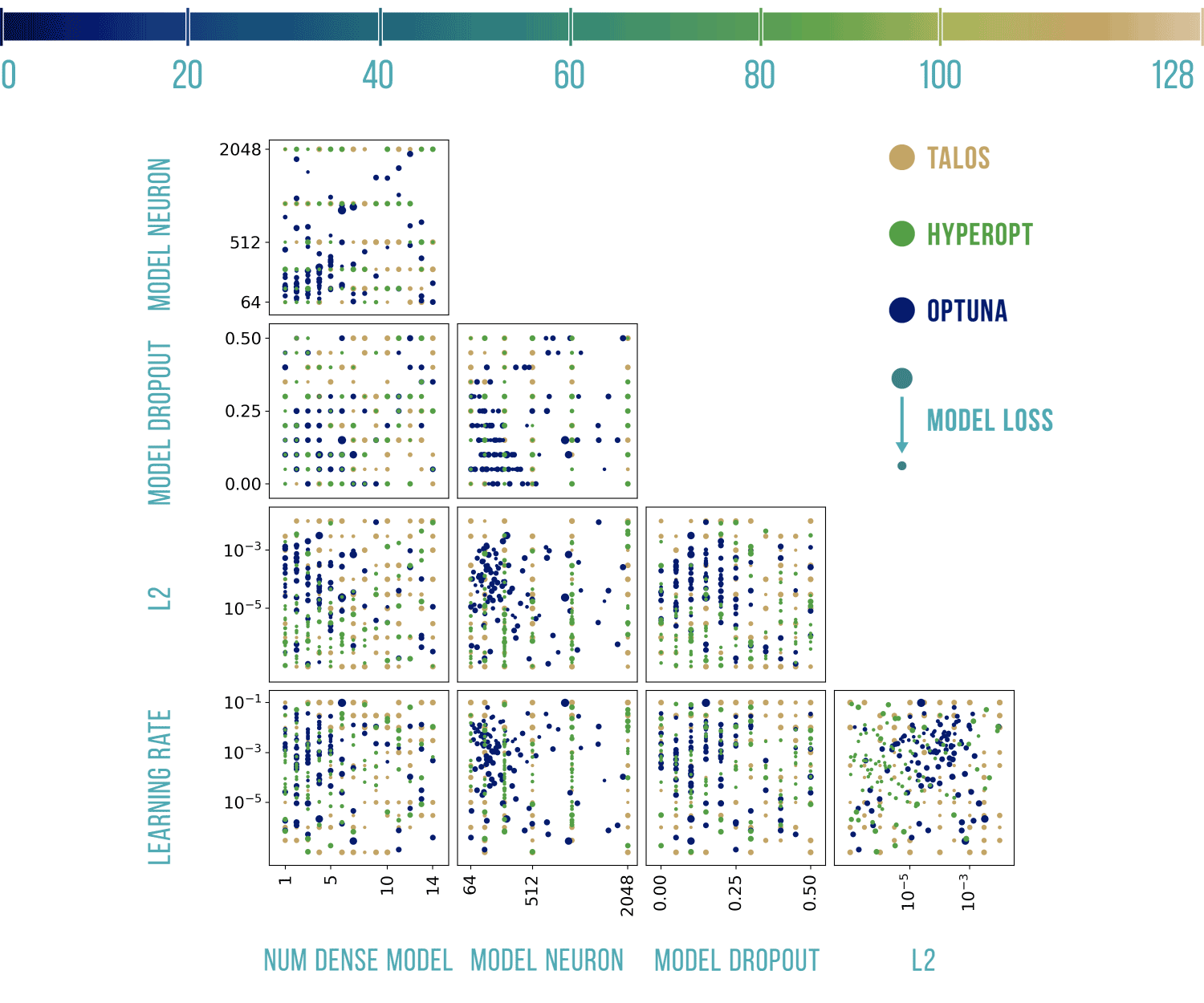
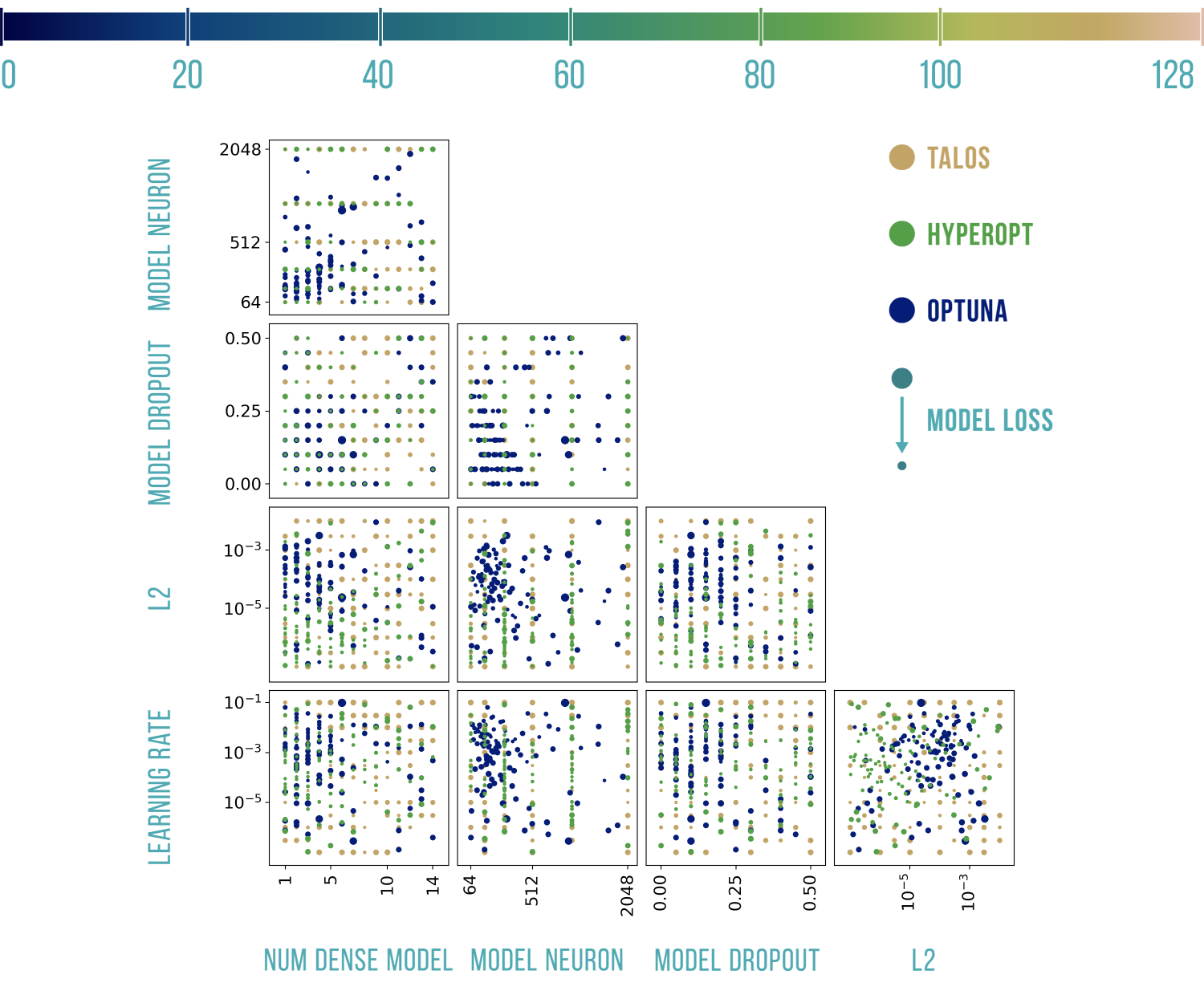
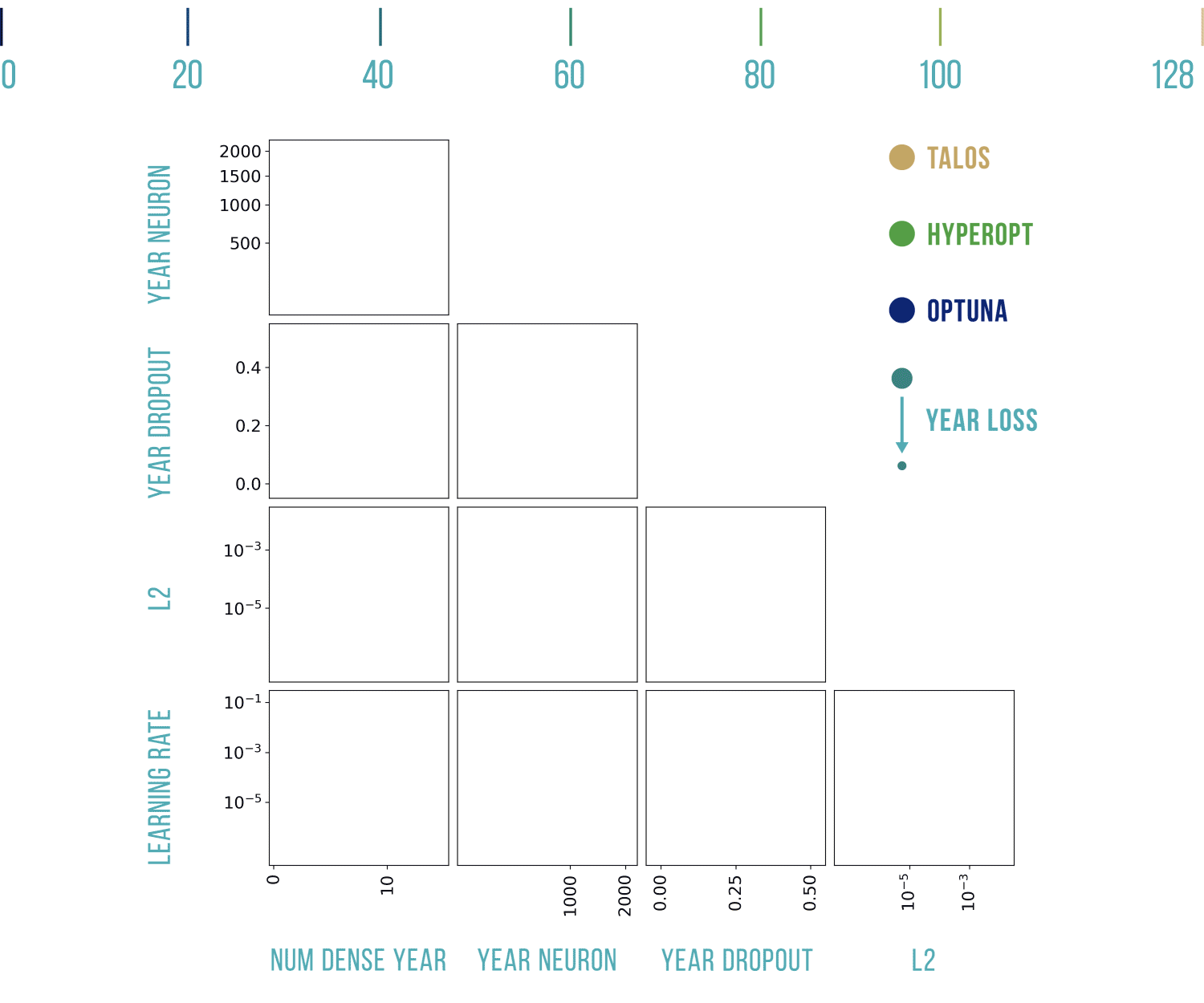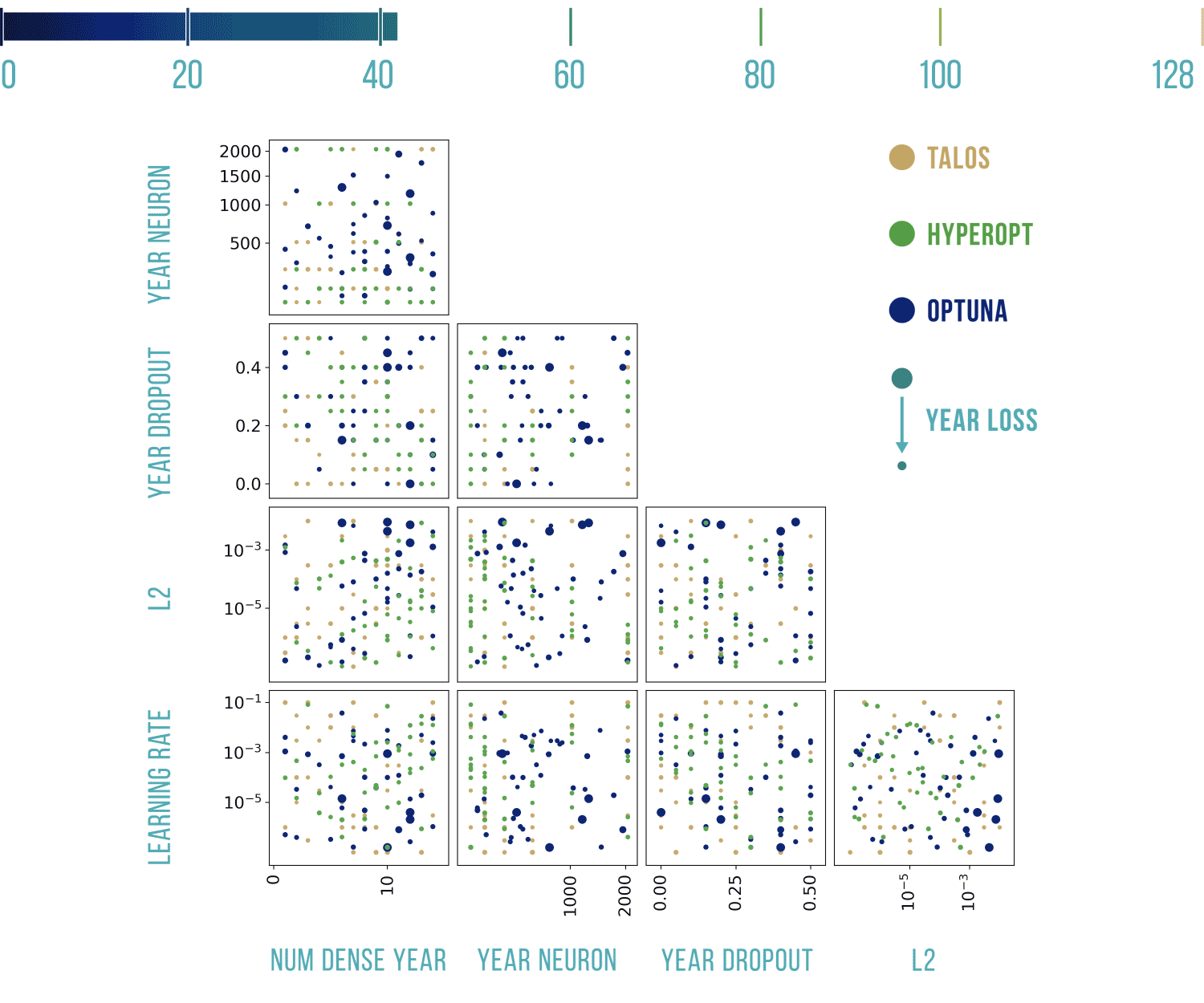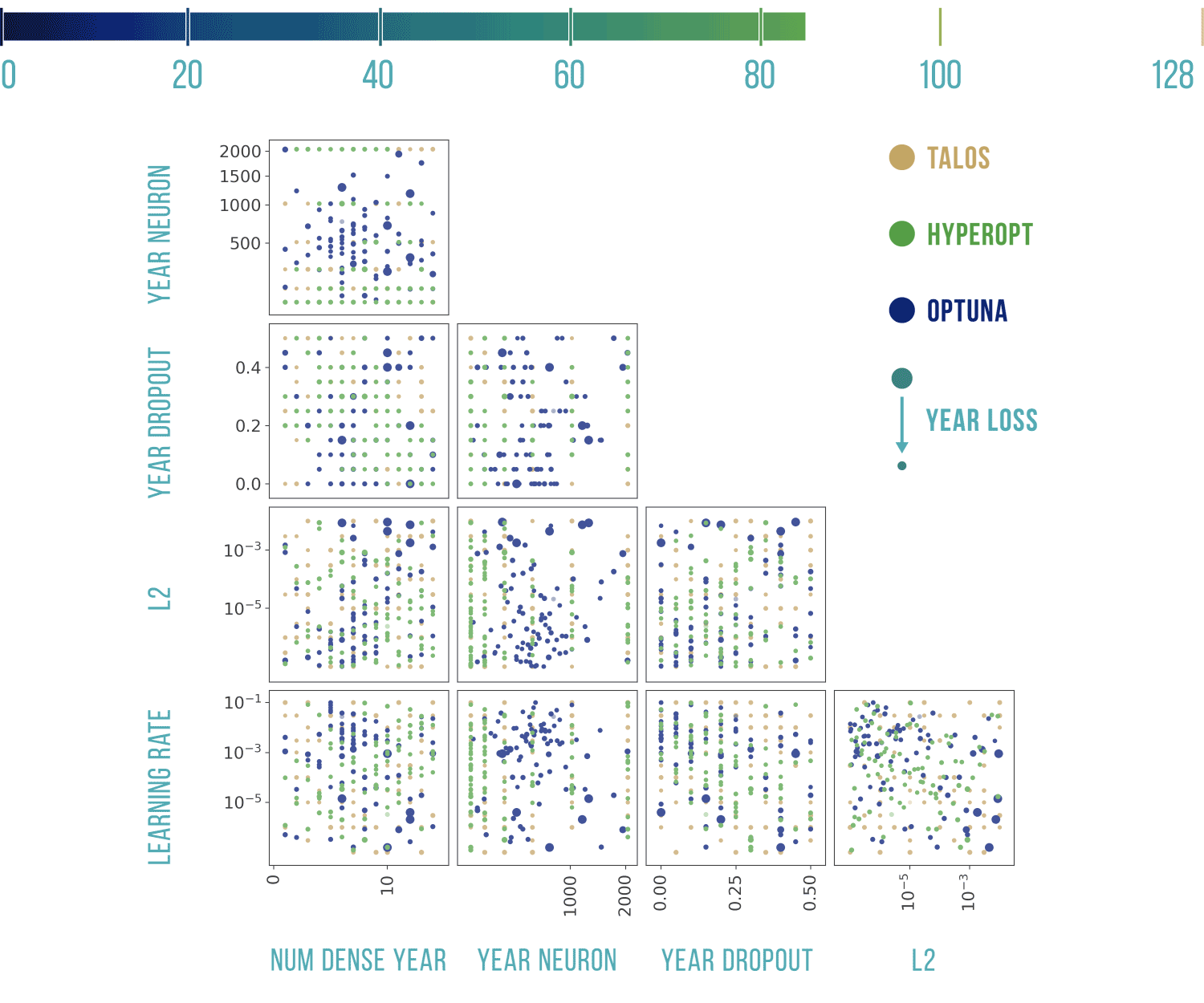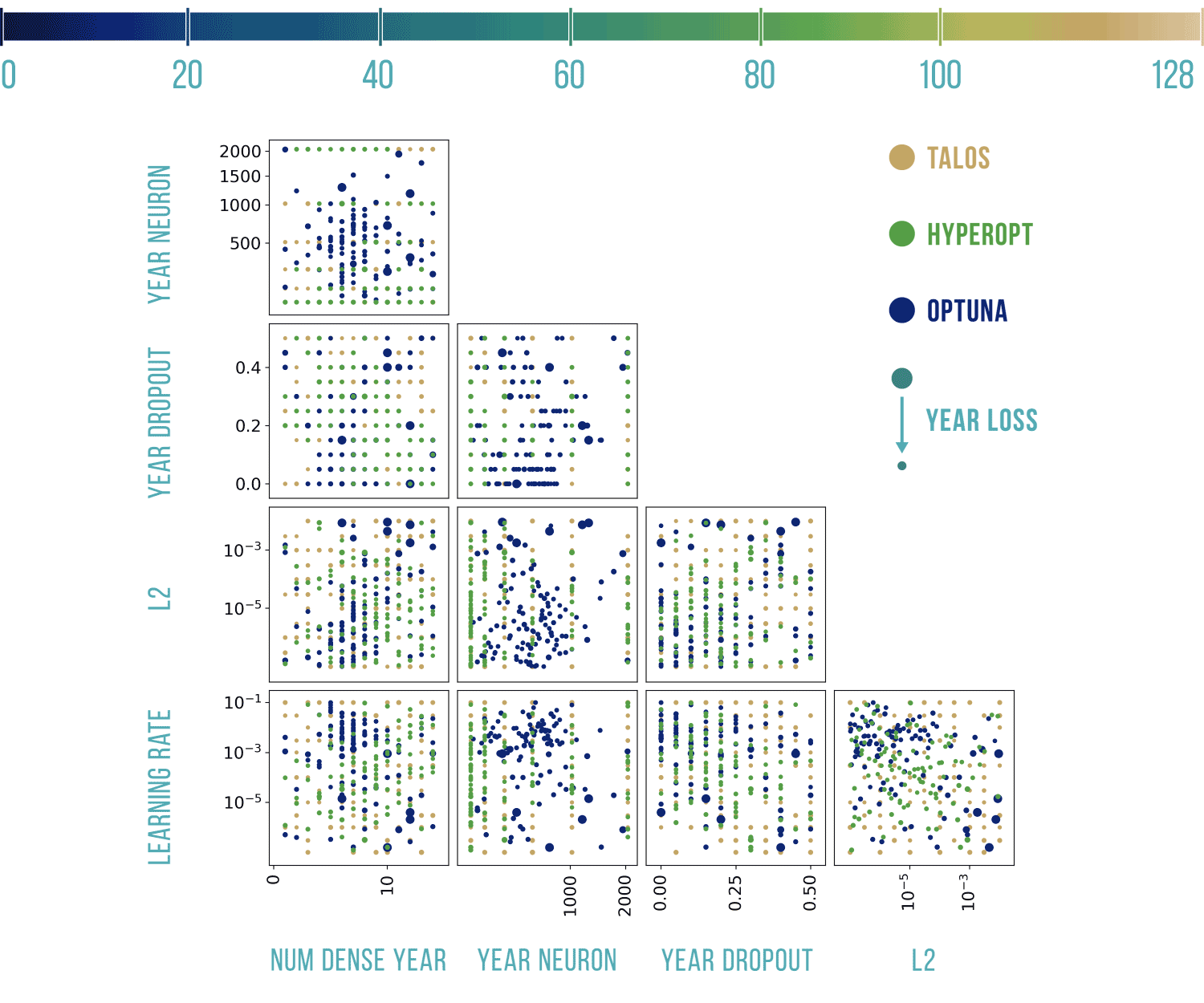
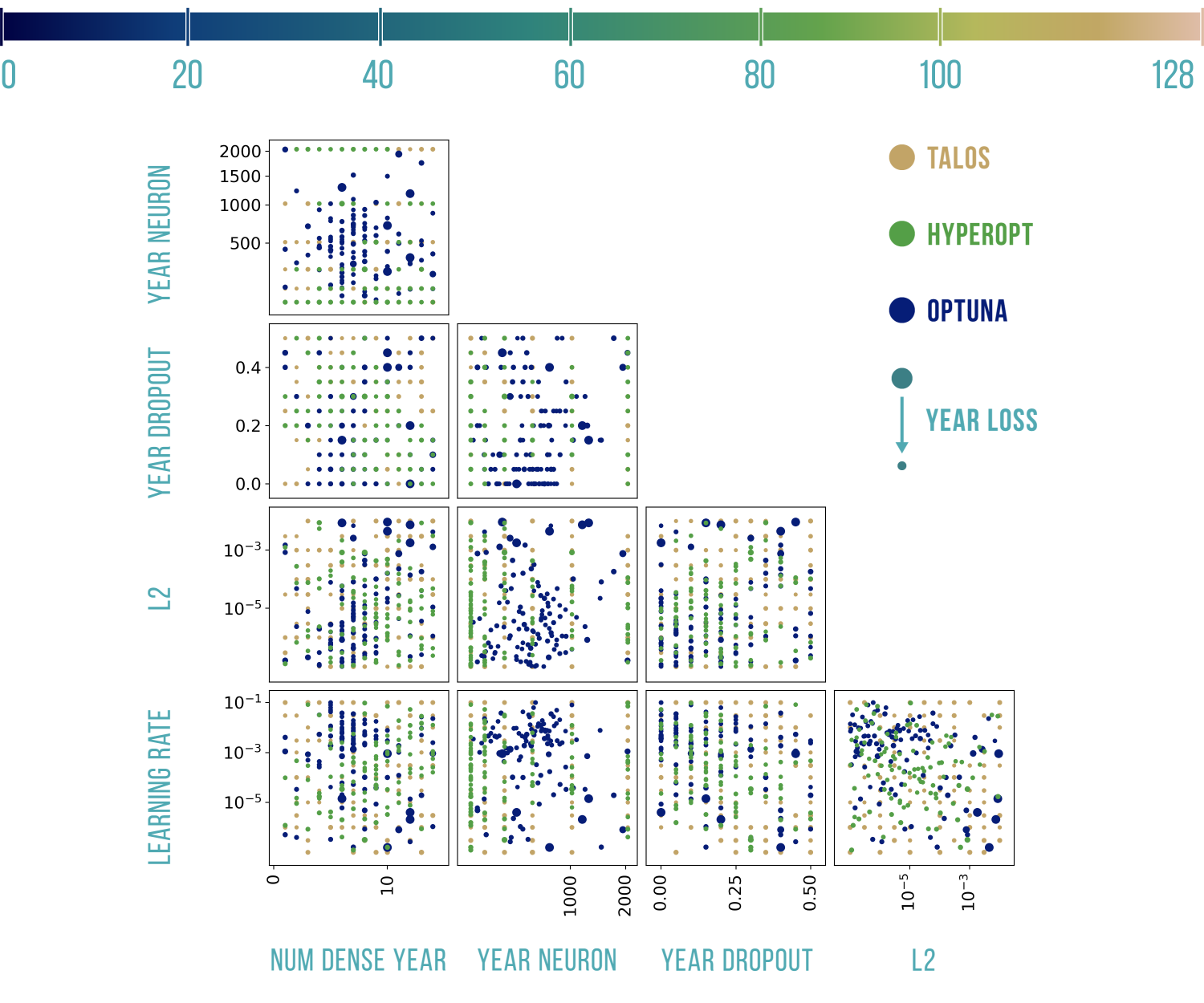
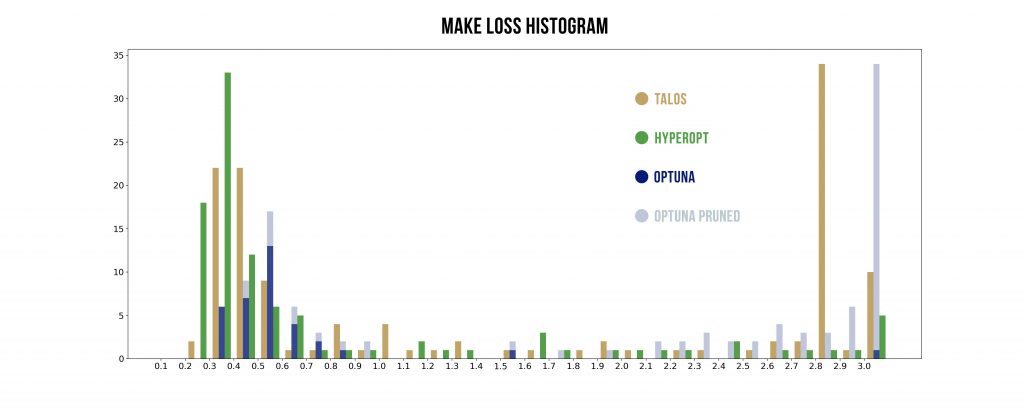
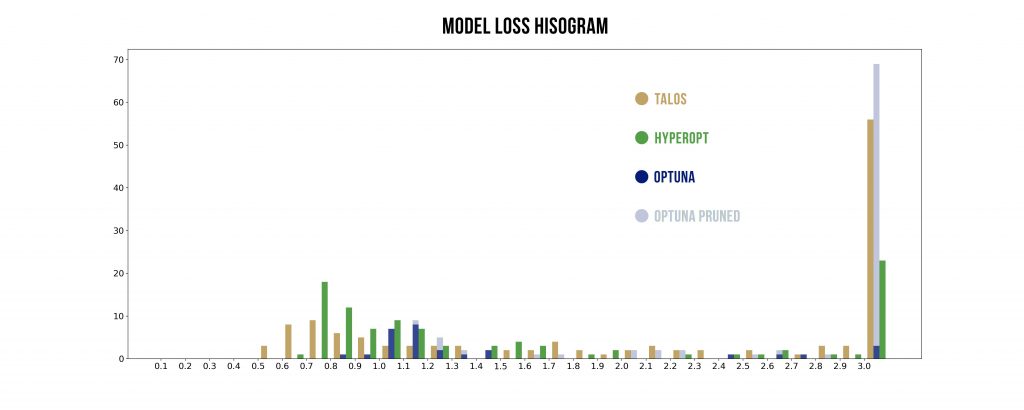
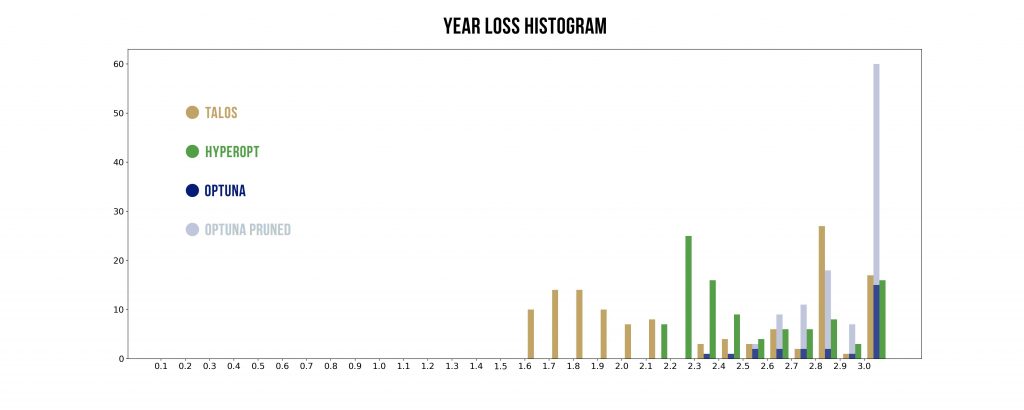
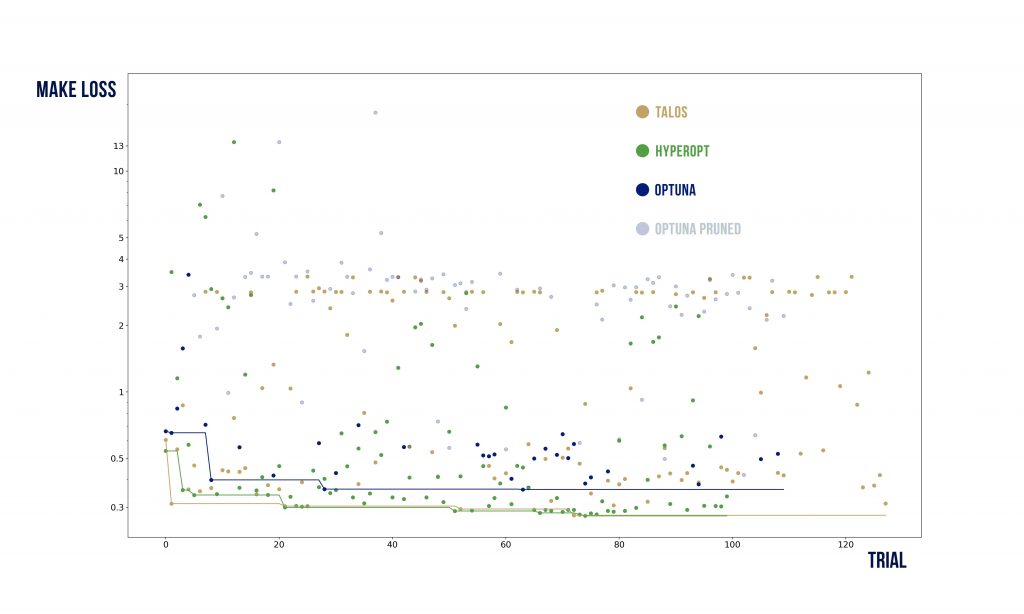
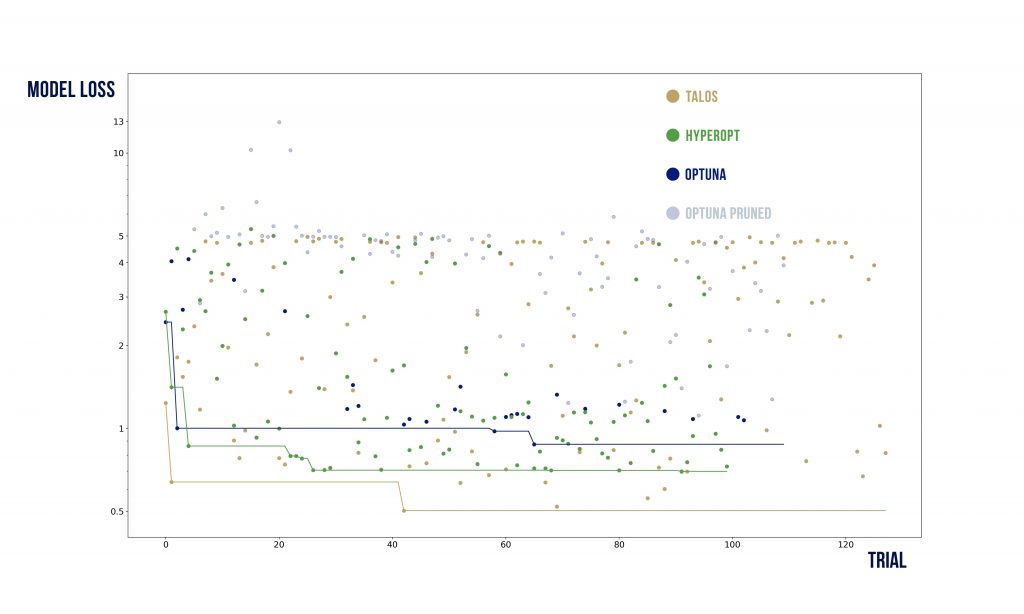
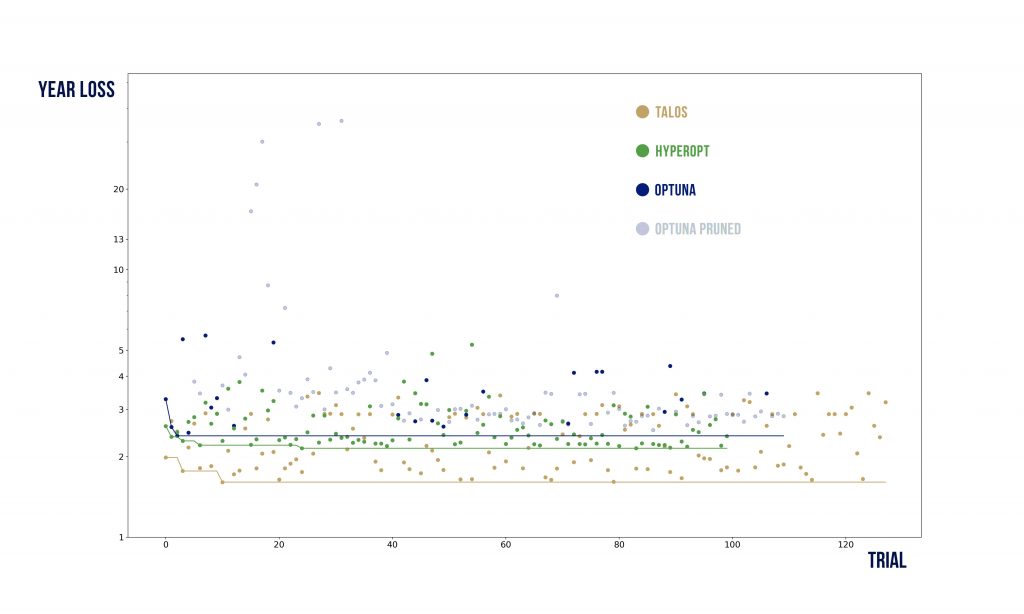
Podstawowy szablon do poniższych wykresów pochodzi stąd: https://benalexkeen.com/parallel-coordinates-in-matplotlib/.
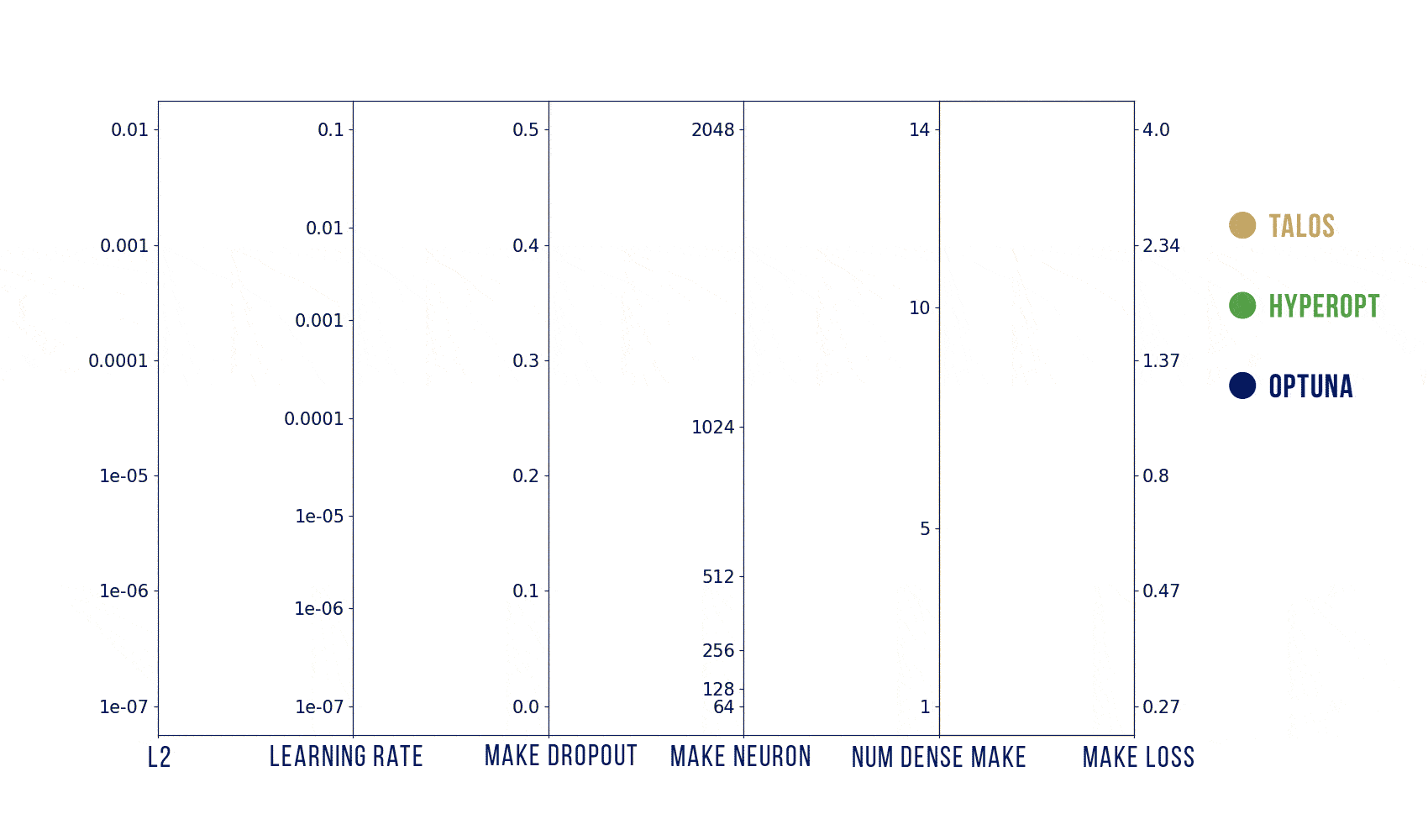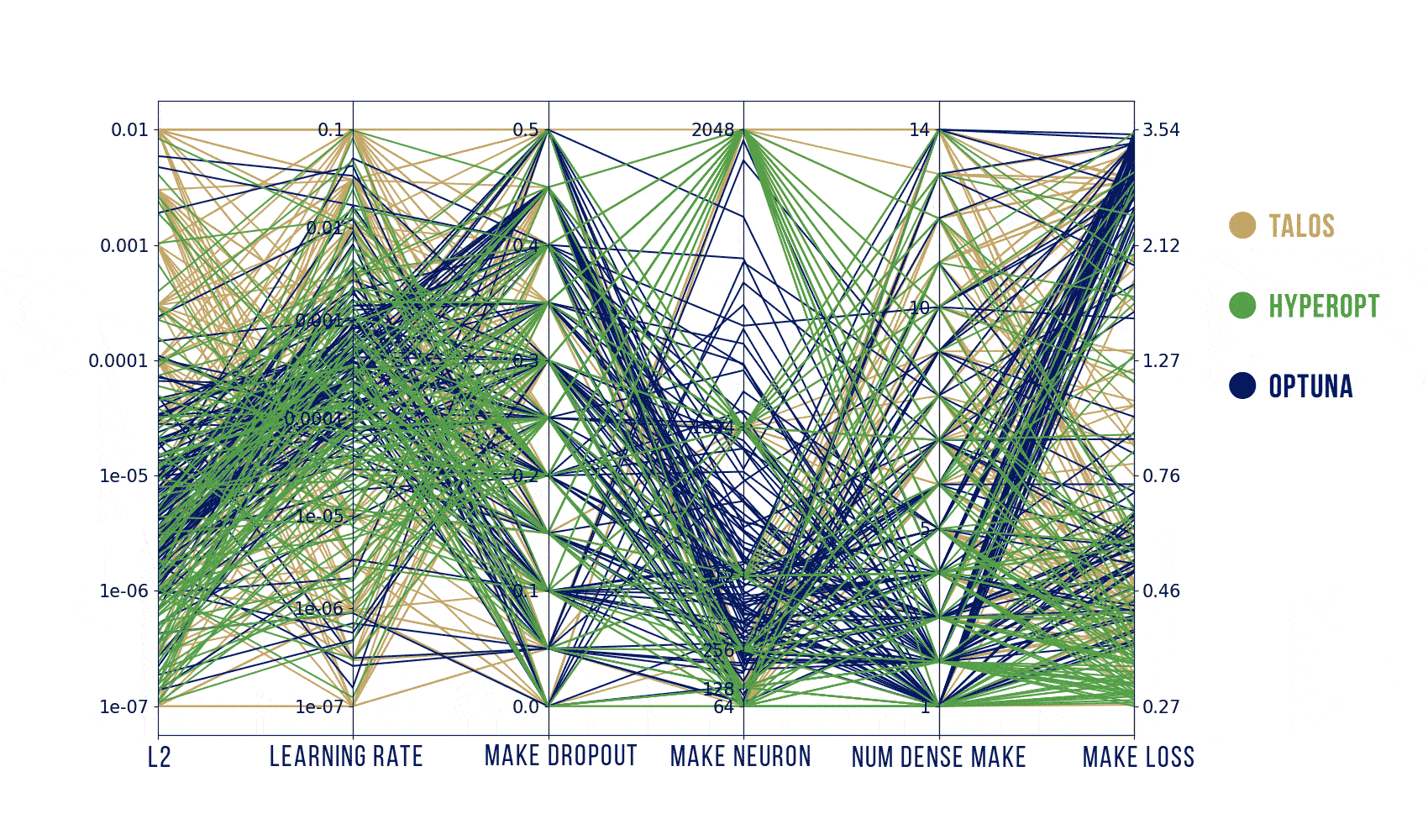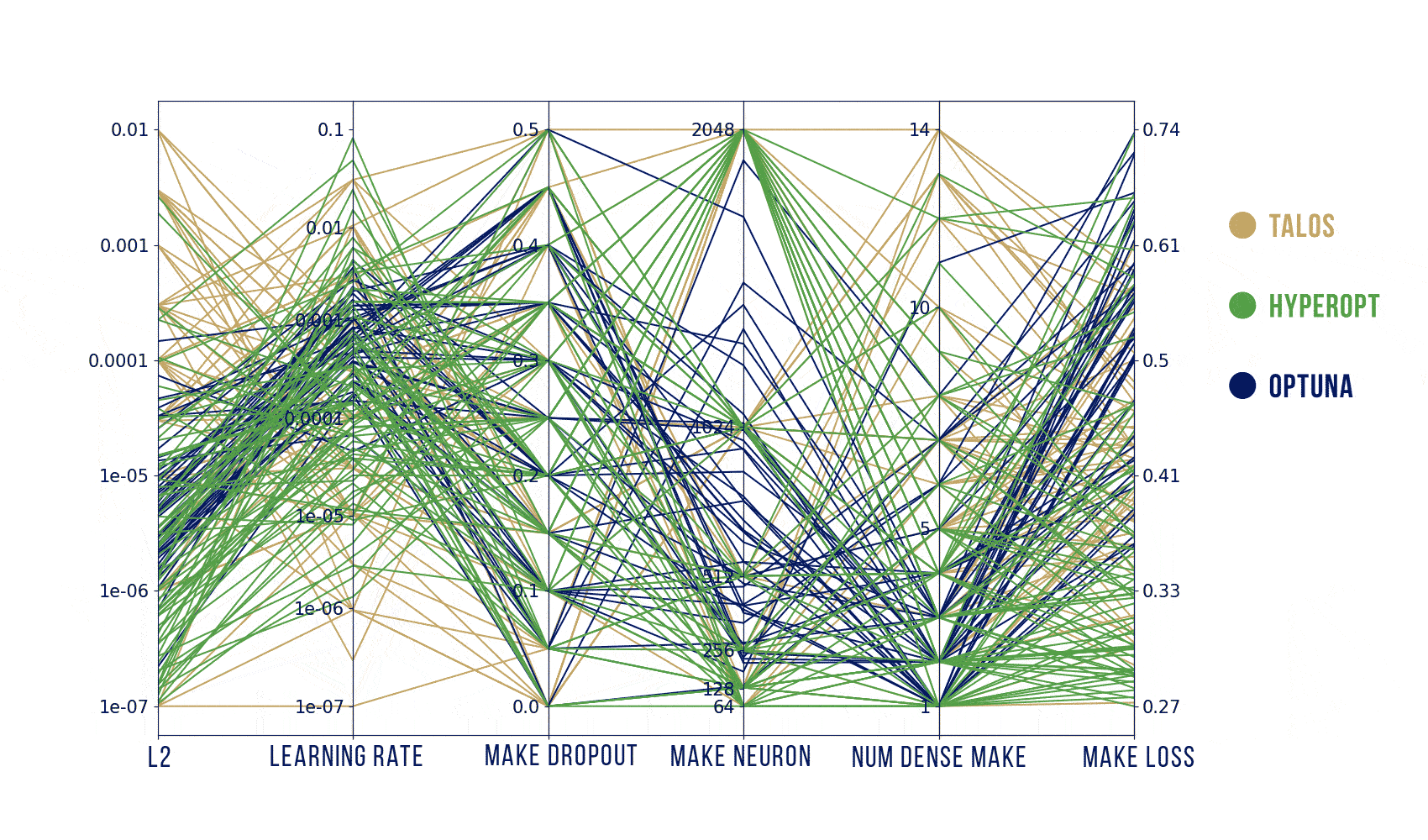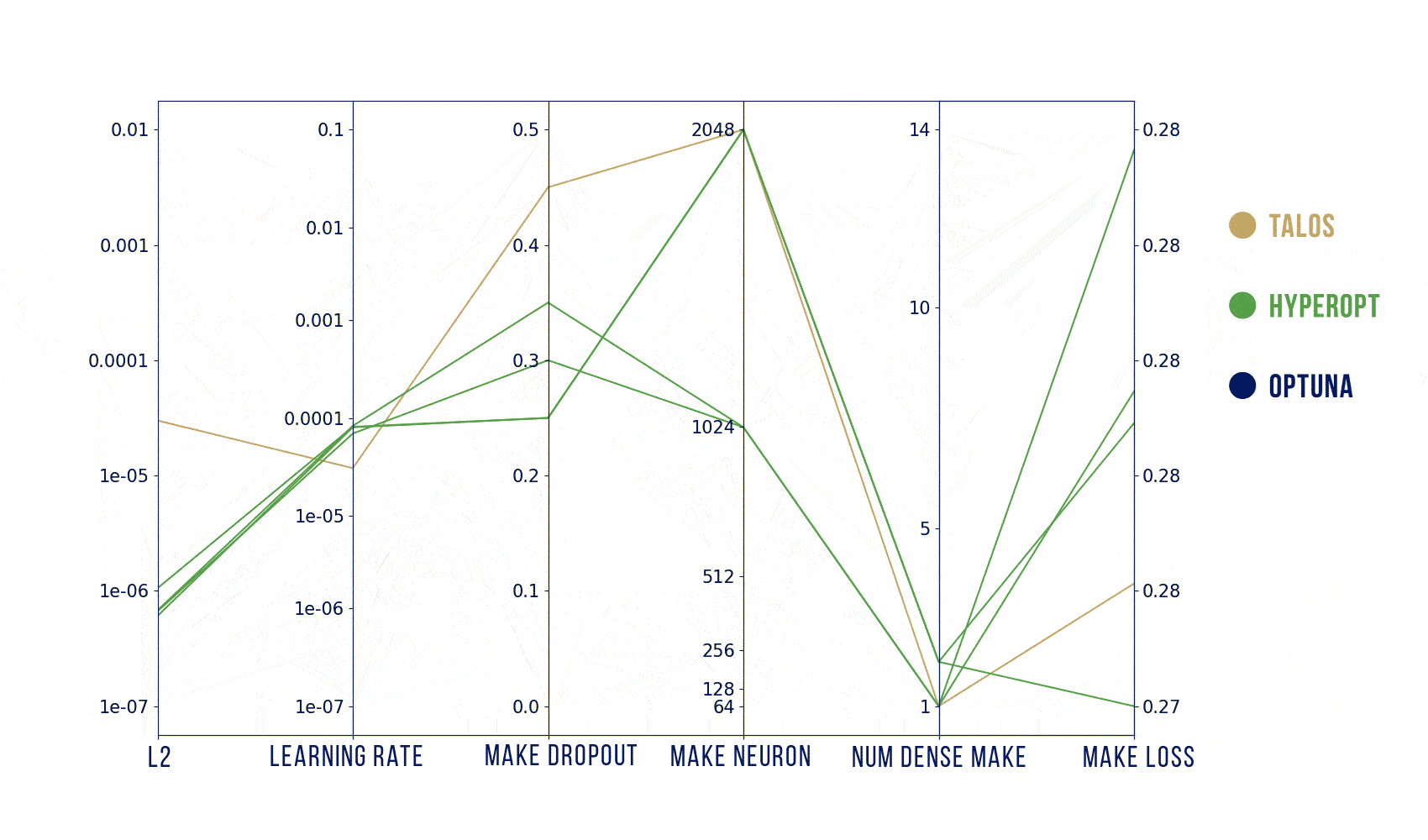
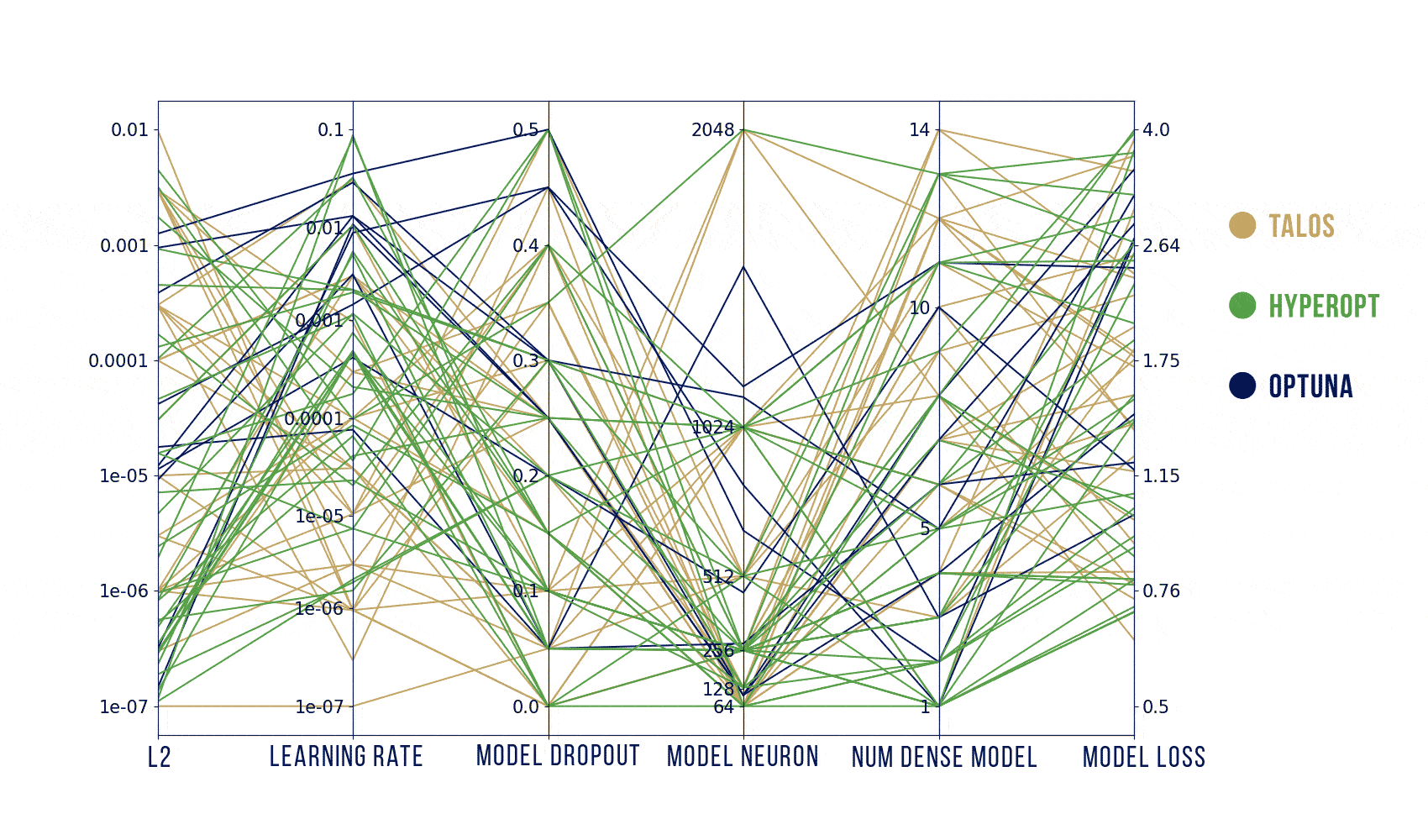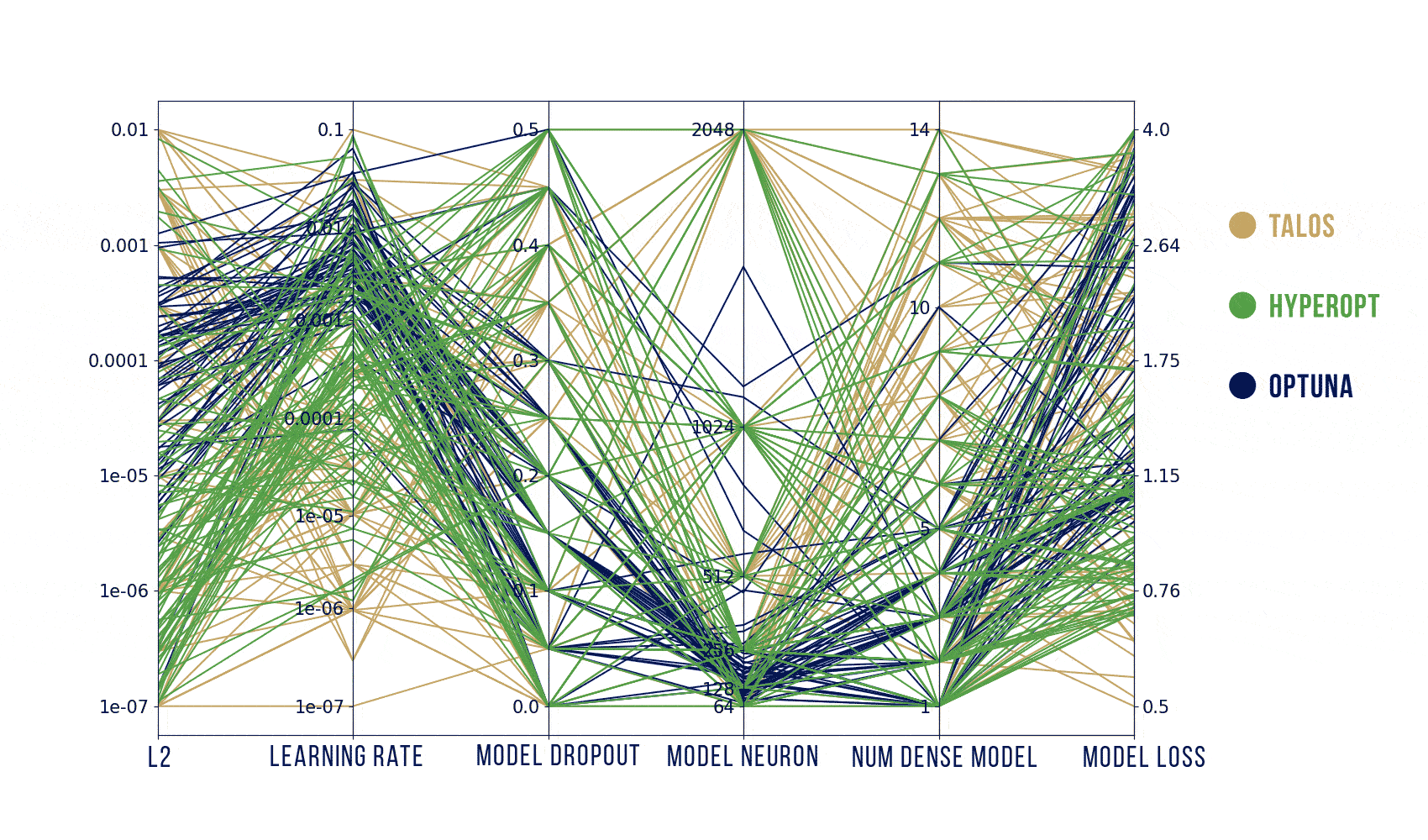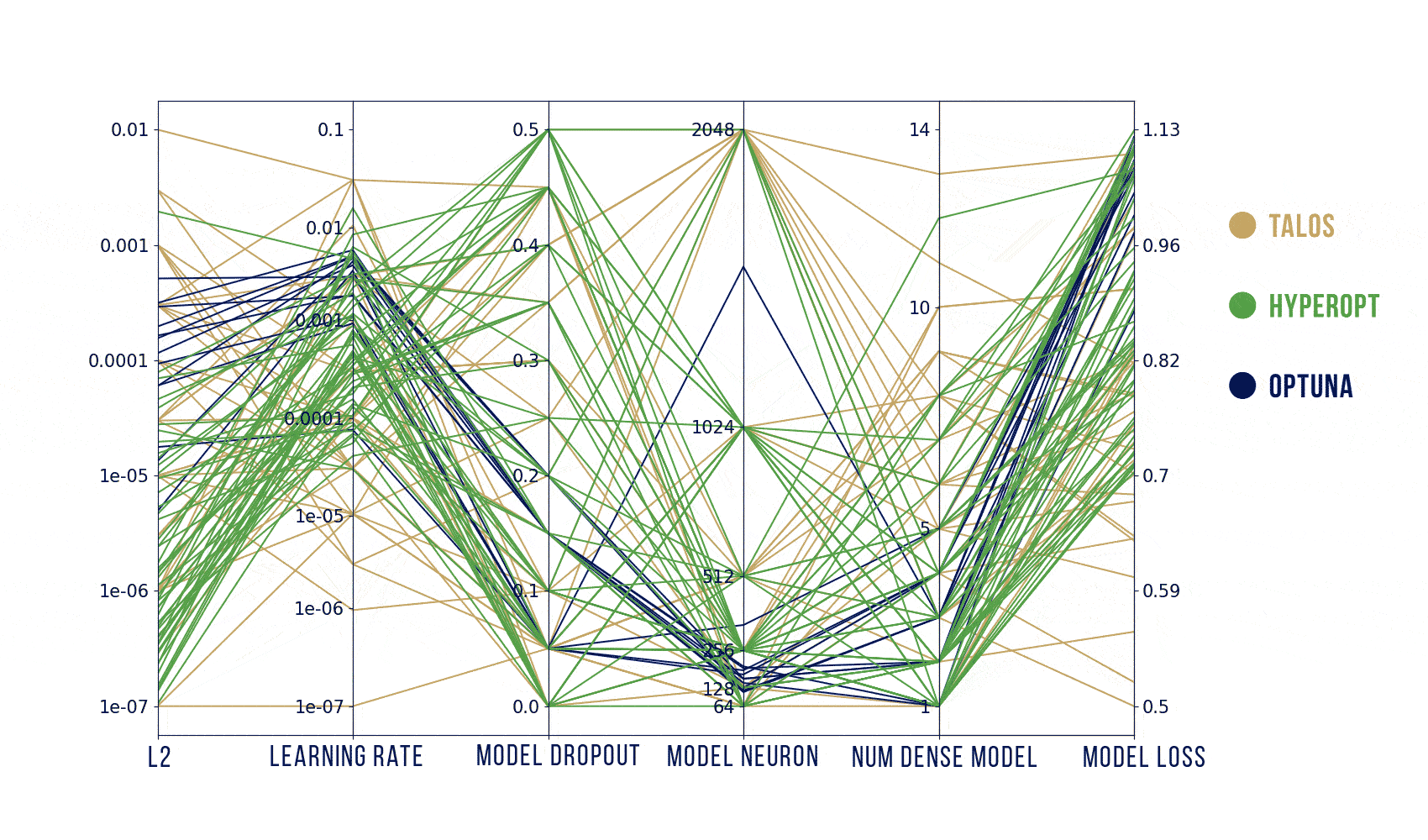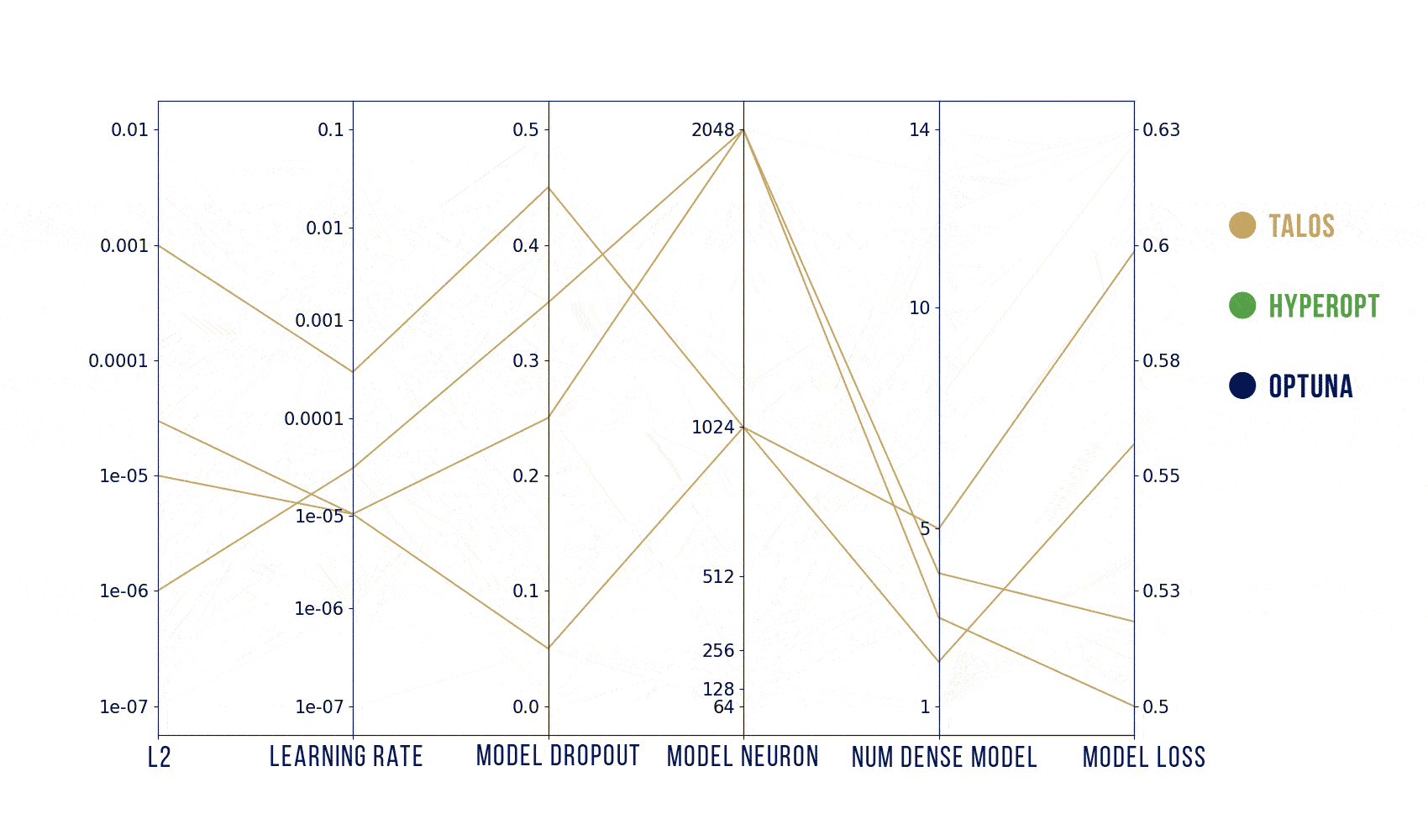
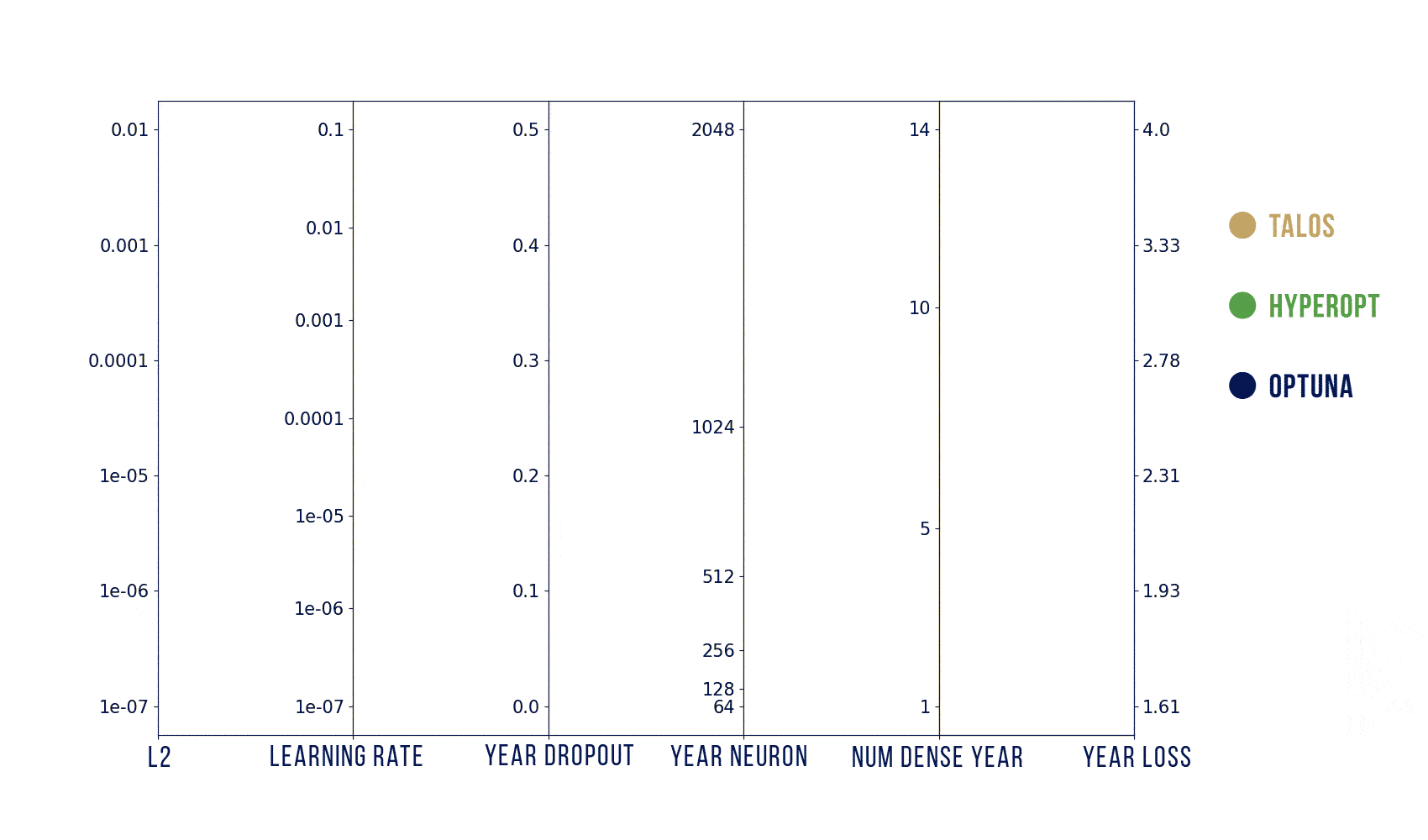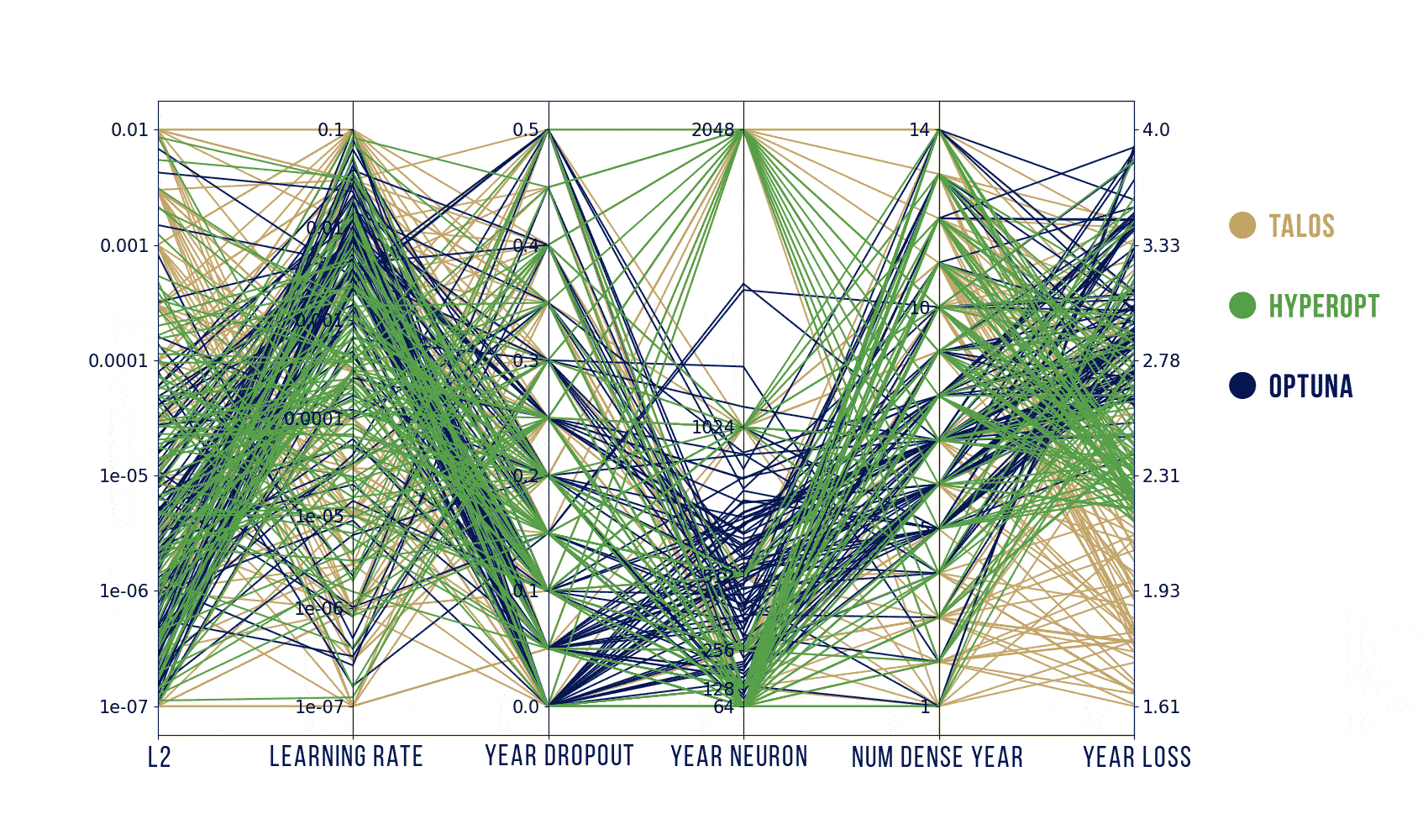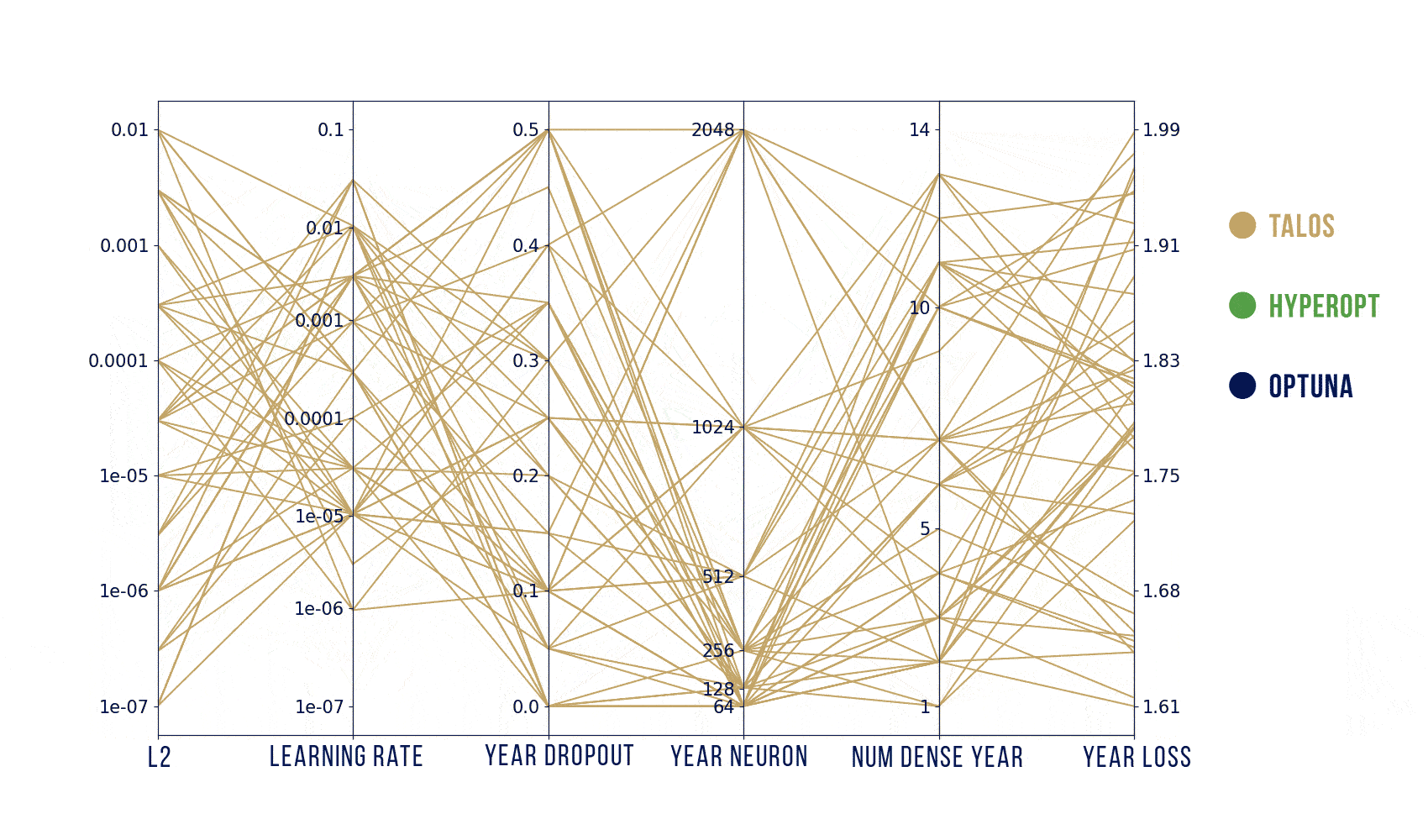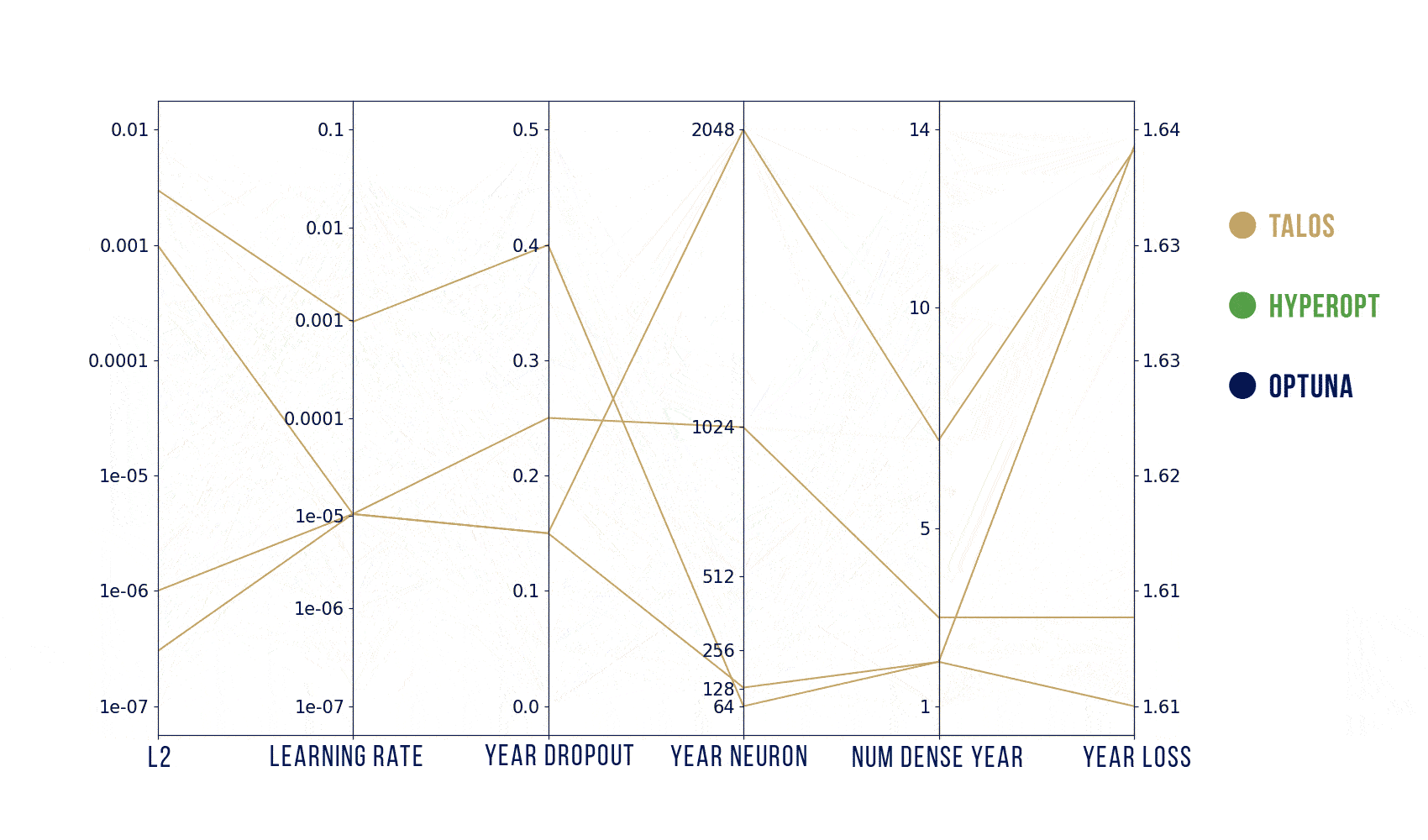
Podsumowanie
Według moich testów, to jak dobre parametry znajdziemy zależy bardziej od tego, jak dobrze zaplanujemy poszukiwania, a nie od samego algorytmu. Szukanych było jednocześnie od 5 parametrów (Hyperopt) do maksymalnie 31 (Optuna) więc liczba losowych prób powinna być znacznie większa niż domyślnie (ogólnie, teoretycznie, powinna rosnąć wykładniczo wraz z liczbą parametrów).
Podsumowując: najwygodniejszym z tych narzędzi jest dla mnie Optuna – używa obydwu algorytmów: random search i estymatora Parzena, a jednocześnie jest znacznie szybszy dzięki wcześniejszemu kończeniu nierokujących prób. Jeśli jednak zależałoby mi na ładnym i szybkim obejrzeniu wyników (także oglądaniu na bieżąco) to zdecydowałabym się na wizualizację z HParams.
Ciekawe linki zewnętrzne
Dotyczące narzędzi
- Optuna vs Hyperopt: Which Hyperparameter Optimization Library Should You Choose? – Jakub Czakon
- An Introductory Example of Bayesian Optimization in Python with Hyperopt – Will Koehrsen
- Optuna: A Next-generation Hyperparameter Optimization Framework – Takuya Akiba, Shotaro Sano, Toshihiko Yanase, Takeru Ohta and Masanori Koyama
- HPO in Python – Jakub Czakon
Dotyczące algorytmów
- Algorithms for hyper-parameter optimization – James Bergstra, Remi Bardenet, Yoshua Bengio, Balazs Kegl
- Kernel density estimation and its application – Stanisław Węglarczyk
- Scalable hyperparameter optimization with lazy gaussian processes – Raju Ram, Sabine Müller, Franz-Josef Pfreundt, Nicolas R. Gauger, Janis Keuper
EfficientNet
- EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks – Mingxing Tan, Quoc V. Le
- EfficientNet Keras (and TensorFlow Keras)


