W tym wpisie zajmiemy się prostą klasyfikacją, rozpoznawaniem obrazów medycznych, czyli przypisywaniem do jednej z dość ogólnych kategorii zbioru Medical MNIST. Spróbujemy osiągnąć wynik 0 pomyłek modelu na zbiorze testowym, sprawdzając, które techniki poprawy wyniku zadziałają tu najlepiej. Zadbamy o powtarzalność wyników, porównamy wytrenowane modele, także dla różnych wielkości zdjęć na wejściu. Dodatkowo zrobimy analizę działania by poznać na jakiej podstawie modele podejmują decyzje.
Prac badawczych na temat uczenia maszynowego w medycynie powstaje bardzo wiele, a jednocześnie stosunkowo niewiele rozwiązań jest wdrażanych do praktyki. Powody mogą być różne, w tym nieufność i niezrozumienie, jak działa dany model i czy faktycznie jest efektywny. Uczenie maszynowe w medycynie napotyka także wiele innych problemów. Dostępność danych obrazowych, w szczególności oznaczonych, jest ograniczona. Oznaczanie jest czasochłonne, wymaga wiedzy lekarskiej i doświadczenia. Dane są często niezrównoważone – więcej jest przypadków osób zdrowych niż posiadających dane schorzenie (a już w szczególności chorobę rzadko występującą). Dochodzą tu jeszcze kwestie prywatności i ochrony danych osobowych.
Projekt można znaleźć na GitHubie.
Zbiór danych
Medical MNIST (skracany także jako MedNIST) jest dostępny na GitHubie. Obrazy w zbiorze pochodzą z kilku baz danych (TCIA, RSNA Bone Age Challenge, NIH Chest X-ray dataset) i są już wstępnie przetworzone, tj, wszystkie zostały przekonwertowane z formatu DICOM do jpeg oraz zmniejszone do rozmiaru 64 x 64 piksele.
W Medical MNIST mamy 6 klas (w odróżnieniu od 10 klas w oryginalnym MNIST). Liczba obrazów jest niemal równomiernie rozłożona i w 5 klasach mamy po 10k przykładów, poza BreastMRI: 8954 przykłady.
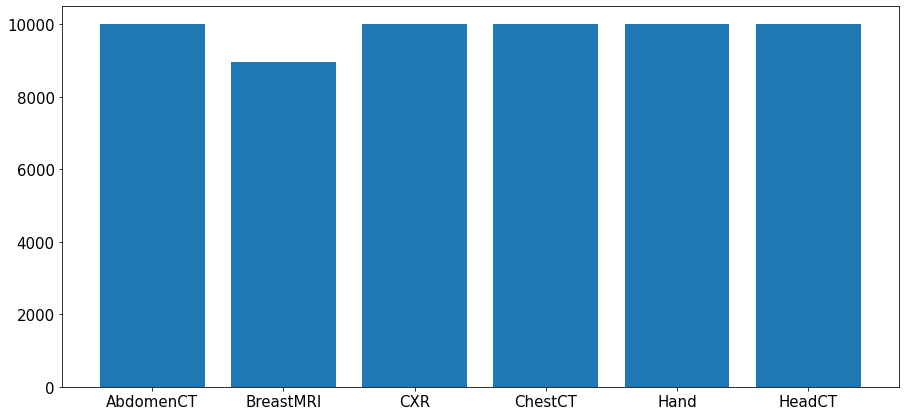
Klasy w zbiorze to:
- AbdomenCT – tomografia komputerowa jamy brzusznej,
- BreastMRI – rezonans magnetyczny piersi,
- CXR – zdjęcie rentgenowskie klatki piersiowej,
- ChestCT – tomografia komputerowa klatki piersiowej,
- Hand – dłoń; bez jawnego wskazania modalności w nazwie etykiety, jednak można z całą pewnością stwierdzić, że jest to zdjęcie rentgenowskie,
- HeadCT – tomografia komputerowa głowy.
Poza liczbą klas Medical MNIST różni się od MNIST jeszcze w paru kwestiach. Jest mniej zdjęć (MedMNIST: 58954, MNIST: 70000) oraz są one większe, w rozmiarze 64 x 64 piksele, a nie 28 x 28. W Medical MNIST przykłady są w formacie jpeg, z kolei oryginalny MNIST jest w formacie idx (służącym do przechowywania wektorów i macierzy).
Wizualizacja obrazów
Aby lepiej zaznajomić się z danymi, zwizualizujmy po kilka przykładów z każdej klasy:






Zobaczmy także uśredniony obraz dla każdej klasy:
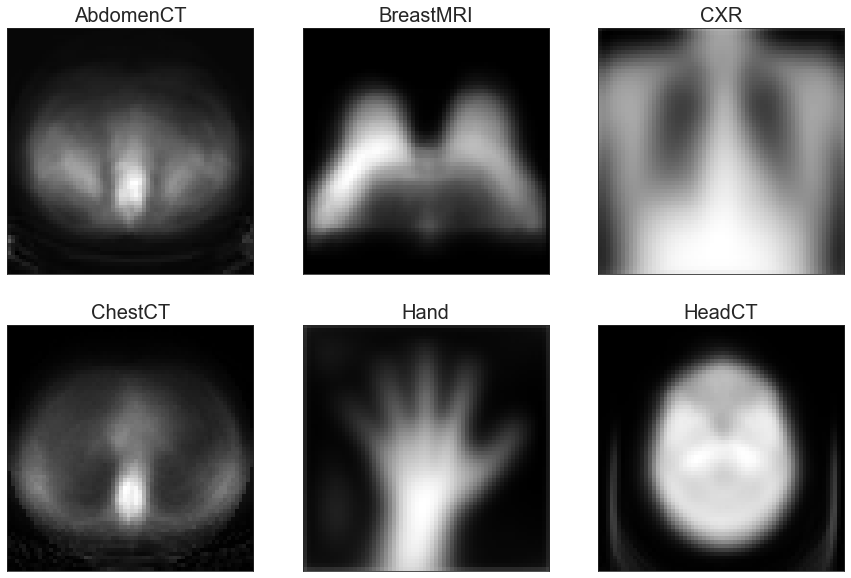
Podobnie wyglądają AbdomenCT oraz ChestCT – kontur ciała jest podobny, widać kręgosłup. Jeśli mielibyśmy na tym etapie wytypować, z którymi klasami model będzie miał największe problemy, zapewne wybralibyśmy właśnie te dwie klasy z uwagi na to podobieństwo. Jednak zdjęcia tomografii komputerowej jamy brzusznej oraz klatki piersiowej można rozróżnić po innych cechach, np. w klatce piersiowej jest serce, a w części brzusznej nie. Zobaczymy, jak poradzi sobie z tym model.
Nietypowe obrazy
W zbiorze znajdują się również obrazy nietypowe, tzn. odróżniające się znacznie od obrazów uśrednionych oraz takie, które bez etykiety bardzo trudno byłoby rozpoznać. Na przykład w klasie Hand zamiast jednej ręki mogą wystąpić obie, w klasie HeadCT może się znaleźć przekrój jedynie z małym fragmentem głowy lub nawet bez żadnego fragmentu.
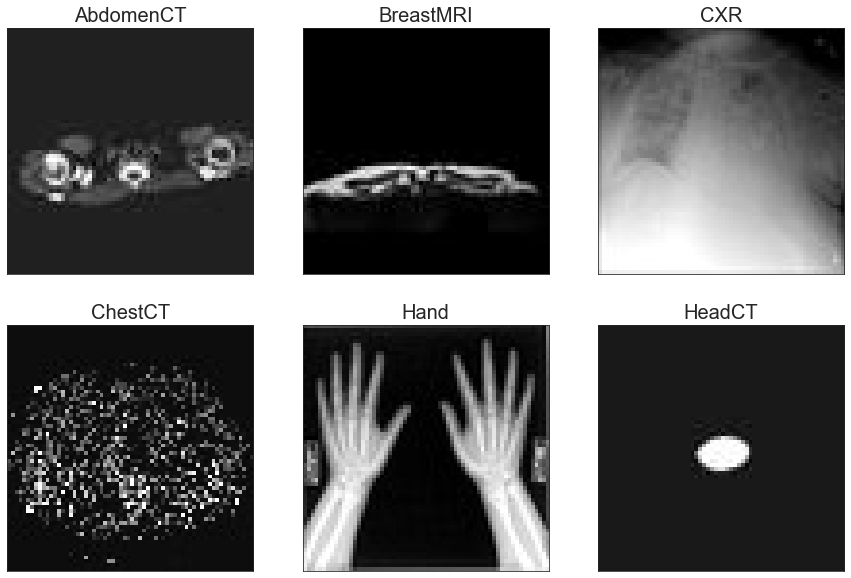
Przygotowanie zbioru dla modelu
Przygotowanie obrazów dla modelu uwzględnia tutaj:
- Podział na zbiór treningowy i testowy – ponieważ zbiór jest w miarę prosty, to możemy podnieść nieco poziom skomplikowania zadania i zachować więcej danych dla zbioru testowego, tj. zrobić podział danych w proporcji 70:30 zamiast 80:20:
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1, stratify=y)

Dla porównania zostały stworzone również zbiory bez użycia opcji stratify:
X_train_v2, X_test_v2, y_train_v2, y_test_v2 = train_test_split(X, y, test_size=0.3, random_state=1)

Startify dba o to, aby proporcje klas po podziale na zbiór treningowy i testowy były takie same jak w zbiorze pierwotnym. Szczególnie przydaje się, gdy jednej klasy jest dużo mniej niż innej. Ponieważ Medical MNIST jest zbiorem w miarę zbalansowanym, to dużej różnicy tu nie widać, jednak zestawmy oba powyższe wykresy obok siebie:

Widać, że dla zbiorów po podziale z użyciem stratify proporcje są zachowane, szczególnie wyraźnie to widać dla klas, które mają 10k wszystkich przykładów – do zbioru treningowego za każdym razem trafia równo 7k przykładów, czyli 70%. Z kolei bez użycia stratify liczba przykładów w zbiorze treningowym jest różna dla poszczególnych klas – czasem nieco mniej niż 7k, czasem nieco więcej.
2. Normalizację – piksele mają wartości 0-255, przeskalujemy je do zakresu 0-1:
if np.max(X_train) > 1: X_train = X_train / np.max(X_train)
if np.max(X_test) > 1: X_test = X_test / np.max(X_test)
3. Dodanie informacji o liczbie kanałów – domyślnie Tensorflow oczekuje na tensor z liczbą kanałów na ostatniej pozycji (channels last):
if X_train.ndim == 3: X_train = np.expand_dims(X_train, axis=-1)
if X_test.ndim == 3: X_test = np.expand_dims(X_test, axis=-1)
4. Zamianę etykiet na liczby – model wymaga, aby zmienne wyjściowe, podobnie jak wejściowe, były numeryczne:
if y_train.dtype.type is np.str_:
y_train = list(map(lambda x: labels.index(x), y_train))
y_train = np.asarray(y_train)
y_test = list(map(lambda x: labels.index(x), y_test))
y_test = np.asarray(y_test)
5. One-hot encoding dla y_train i y_test – aby nie narzucać etykietom hierarchii, ponieważ dana kolejność ustawienia i numery etykiet nie mają znaczenia (tzn. przykładowo HeadCT zakodowane jako 5 nie jest w żaden sposób „najważniejsze” pośród wszystkich klas, ponieważ ma najwyższy numer):
if y_train.ndim == 1:
y_train = to_categorical(y_train, num_classes)
y_test = to_categorical(y_test, num_classes)
Data augmentation
Mając mało danych lub chcąc rozwiązać problem przeuczenia, można sztucznie powiększyć zbiór danych. Należy to jednak robić rozsądnie i brać pod uwagę specyfikę danego zadania. W przypadku obrazów medycznych nie każde przekształcenie będzie zawsze uzasadnione. Przykładowo: dla Medical MNIST, gdy klasyfikujemy obraz jako całość do jednej z ogólnych kategorii, odbicie poziome jest w porządku. W innym przypadku jednak (m.in. problem lokalizacji różnych zmian patologicznych na obrazie) mogłoby wprowadzić model w błąd i wpłynąć na wynik – na przykład obraz klatki piersiowej/jamy brzusznej po odbiciu poziomym przedstawia tzw. odwrócenie trzewi (sytuacja, w której narządy wewnętrzne znajdują się po przeciwnych stronach niż ich prawidłowe położenie).
Żeby sprawdzić, jak data augmentation wpływa na wynik dla Medical MNIST, wybierzmy kilka przekształceń: odbicie poziome, powiększenie fragmentu, obrót o nie więcej niż 30° i obrót o nie więcej niż 180°. W zbiorze oryginalnym znajdują się już obrazy, które są na przykład obrócone i model się przy nich myli (niżej w sekcji Podstawowy model można zobaczyć przykład takich źle sklasyfikowanych Hand i CXR), więc więcej podobnych zdjęć w zbiorze treningowym może również pomóc i w tej kwestii.

Podstawowy model
Podstawową architekturą będzie architektura zaproponowana w tym samouczku.
model = Sequential([
Conv2D(32, (3,3), activation='relu', input_shape=input_shape),
MaxPooling2D((2,2)),
Conv2D(64, (3,3), activation='relu'),
MaxPooling2D((2,2)),
Conv2D(64, (3,3), activation='relu'),
Flatten(),
Dense(64, activation='relu'),
Dense(num_classes, activation='softmax')
])
| Layer (type) | Output shape | Param # |
|---|---|---|
| conv2d (Conv2D) | (None, 62, 62, 32) | 320 |
| max_pooling2d (MaxPooling2D) | (None, 31, 31, 32) | 0 |
| conv2d_1 (Conv2D) | (None, 29, 29, 64) | 18496 |
| max_pooling2d_1 (MaxPooling2D) | (None, 14, 14, 64) | 0 |
| conv2d_2 (Conv2D) | (None, 12, 12, 64) | 36928 |
| flatten (Flatten) | (None, 9216) | 0 |
| dense (Dense) | (None, 64) | 589888 |
| dense_1 (Dense) | (None, 6) | 390 |
| Total params: 646,022 Trainable params: 646,022 Non-trainable params: 0 |
Model trenujemy przez 30 epok 100 razy (dlaczego – o tym w sekcji Powtarzalność wyników poniżej).
model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])
history = model.fit(X_train, y_train, epochs=30, validation_data=(X_test, y_test))
Udało się osiągnąć średnio 10 pomyłek (mediana: 10), co ustanawiamy naszym baselinem.
Zerknijmy na macierz pomyłek jednej z iteracji oraz zwizualizujmy, jakie błędy model popełnia.
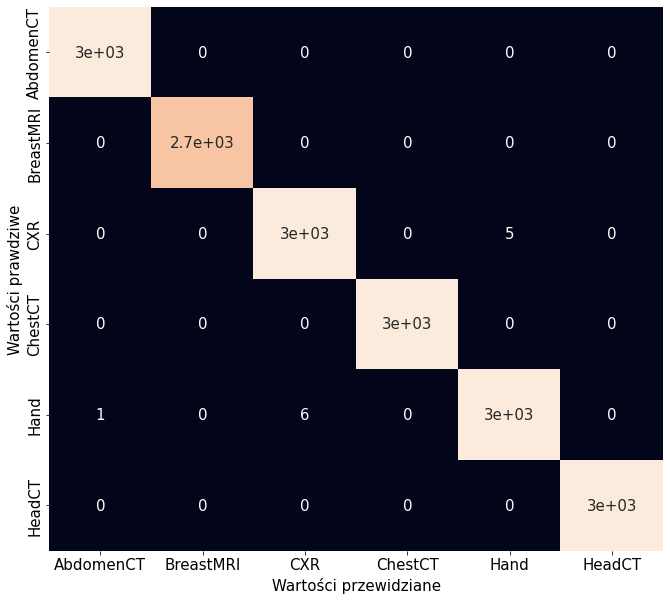
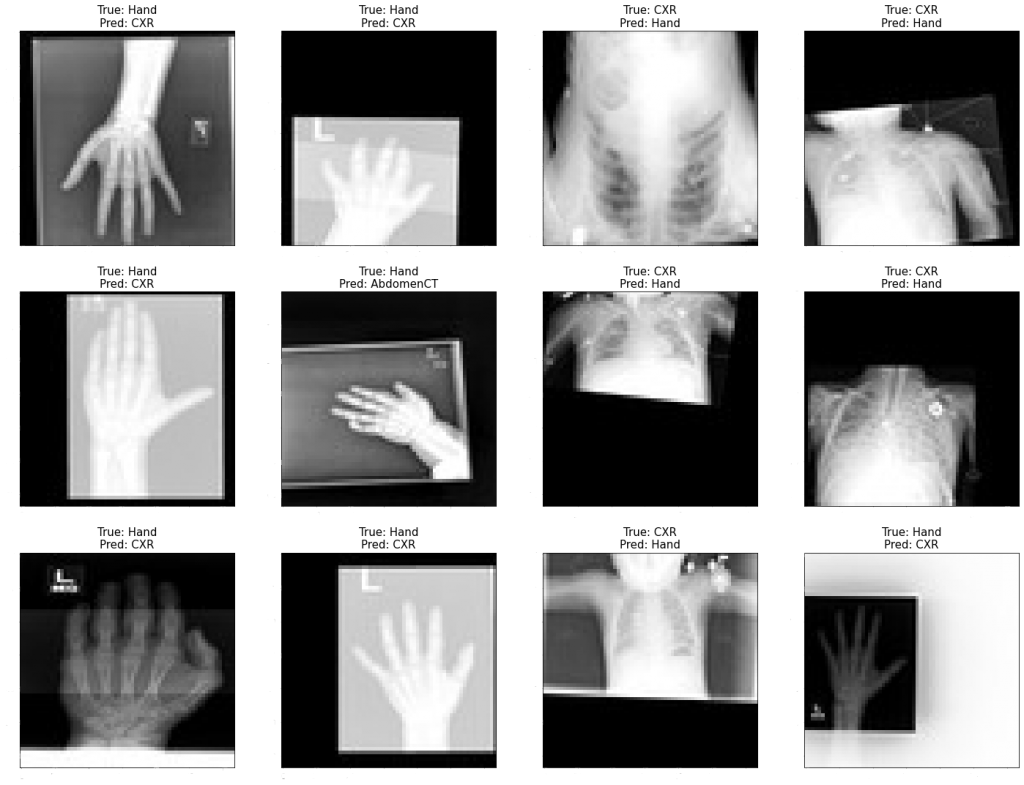
Model najwięcej błędów popełnia przy rozpoznawaniu Hand/CXR. Tak się dzieje dla każdej iteracji. Nawet AbdomenCT i ChestCT są poprawnie klasyfikowane w zdecydowanej większości przypadków, mimo że można by się było spodziewać inaczej po początkowym zerknięciu na dane.
Powtarzalność wyników
Sieci neuronowe są z natury stochastyczne (wagi są inicjowane losowo, niektóre ich komponenty, jak na przykład dropout, działają również w sposób losowy), więc każde kompilowanie i trenowanie modelu od początku przy użyciu tych samych danych może dawać różne wyniki. Czasem chcemy, aby tak było, jednak na etapie tworzenia i rozwijania modelu losowość nie jest wskazana, gdyż przeszkadza w ocenie, czy nasze wysiłki poprawiają czy pogarszają wyniki.
Chcąc zagwarantować sobie powtarzalność wyników, można skorzystać z podpowiedzi w dokumentacji Kerasa. Jednym ze sposobów jest ustawienie zmiennej środowiskowej PYTHONHASHSEED na 0 przed uruchomieniem programu. Kolejnym sposobem jest ustawienie ziarenek (seed) dla każdego z modułów, z których korzystamy w projekcie:
random.seed(1)
np.random.seed(1)
tf.random.set_seed(1)
Powtarzalność wyników jest również uzależniona od procesora. Jeśli jest używany procesor graficzny (GPU), to powtarzalność nie jest zagwarantowana, ponieważ GPU wykonuje wiele operacji jednocześnie, niekoniecznie w tej samej kolejności za każdym razem. Poniżej są przedstawione wyniki z 5 iteracji trenowania modelu przez 1 epokę na zmniejszonym zbiorze treningowym dla dwóch przypadków – z użyciem CPU oraz z użyciem GPU:
CPU
258/258 [==============================] - 64s 250ms/step - loss: 0.1652 - accuracy: 0.9441 - val_loss: 0.0414 - val_accuracy: 0.9880
Iteration: 1 Mistakes: 213
258/258 [==============================] - 65s 252ms/step - loss: 0.1652 - accuracy: 0.9441 - val_loss: 0.0414 - val_accuracy: 0.9880
Iteration: 2 Mistakes: 213
258/258 [==============================] - 63s 243ms/step - loss: 0.1652 - accuracy: 0.9441 - val_loss: 0.0414 - val_accuracy: 0.9880
Iteration: 3 Mistakes: 213
258/258 [==============================] - 63s 244ms/step - loss: 0.1652 - accuracy: 0.9441 - val_loss: 0.0414 - val_accuracy: 0.9880
Iteration: 4 Mistakes: 213
258/258 [==============================] - 63s 246ms/step - loss: 0.1652 - accuracy: 0.9441 - val_loss: 0.0414 - val_accuracy: 0.9880
Iteration: 5 Mistakes: 213
GPU
258/258 [==============================] - 6s 22ms/step - loss: 0.1955 - accuracy: 0.9369 - val_loss: 0.0227 - val_accuracy: 0.9955
Iteration: 1 Mistakes: 79
258/258 [==============================] - 5s 21ms/step - loss: 0.1934 - accuracy: 0.9360 - val_loss: 0.0337 - val_accuracy: 0.9919
Iteration: 2 Mistakes: 144
258/258 [==============================] - 5s 20ms/step - loss: 0.1871 - accuracy: 0.9368 - val_loss: 0.0260 - val_accuracy: 0.9943
Iteration: 3 Mistakes: 100
258/258 [==============================] - 5s 21ms/step - loss: 0.1812 - accuracy: 0.9366 - val_loss: 0.0668 - val_accuracy: 0.9818
Iteration: 4 Mistakes: 322
258/258 [==============================] - 5s 20ms/step - loss: 0.1884 - accuracy: 0.9337 - val_loss: 0.0288 - val_accuracy: 0.9910
Iteration: 5 Mistakes: 160
Liczba pomyłek oraz pozostałe metryki, accuracy i loss, w przypadku CPU są stabilne. W przypadku GPU w każdej iteracji dostajemy inny wynik, co potwierdza, że powtarzalność wyników została osiągnięta do momentu, gdy chcemy użyć GPU. Przy okazji widzimy, że z użyciem GPU model trenuje się szybciej. Jeżeli mamy czas i nieduży model, możemy rozważyć używanie CPU, dzięki czemu dostaniemy w każdej iteracji taki sam wynik.
Pracując na GPU i chcąc wyciągać odpowiednie wnioski na podstawie uzyskiwanych wyników, należy powtórzyć dany eksperyment wiele razy (tutaj: 100), a następnie przyjrzeć się rozkładowi wyników. Przedstawiając ostateczny wynik dla danych parametrów i architektury modelu, można podać na przykład średnią oraz odchylenie standardowe lub medianę (jak w tabeli w następnej sekcji).
Eksperymenty
Aby polepszyć wynik i zapobiec przeuczeniu, zastosujmy kilka technik. Wyniki eksperymentów zostały zebrane w poniższej tabelce. Z uwagi na wspomnianą wyżej niepowtarzalność wyników każdy model był trenowany od początku 100 razy przez 30 epok. Następnie na podstawie wyników z tych 100 treningów została policzona średnia oraz mediana pomyłek każdego modelu. W pierwszej kolejności były sprawdzane modele z pojedynczymi modyfikacjami względem modelu podstawowego, a następnie łączono ze sobą modyfikacje, które poprawiały wynik baseline’u.
| Model | Rozmiar obrazów 32 x 32 | Dropout w części Dense | Global MaxPooling | Odbicie poziome | Powiększenie | Obrót <= 30° | Obrót <= 180° | Batch Normalization | Średnia liczba pomyłek modelu | Mediana pomyłek modelu |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 – baseline | 10 ± 2 | 10 | ||||||||
| 2 | ✓ | 13 ± 4 | 12 | |||||||
| 3 | 0.1 | 12 ± 8 | 10 | |||||||
| 4 | 0.2 | 14 ± 7 | 12 | |||||||
| 5 | 0.3 | 15 ± 6 | 14 | |||||||
| 6 | 2x 0.1 | 22 ± 14 | 19 | |||||||
| 7 | 2x 0.2 | 15 ± 9 | 13 | |||||||
| 8 | 2x 0.3 | 16 ± 16 | 13 | |||||||
| 9 | ✓ | 7 ± 6 | 6 | |||||||
| 10 | ✓ | 7 ± 4 | 7 | |||||||
| 11 | ✓ | 13 ± 7 | 12 | |||||||
| 12 | ✓ | 9 ± 7 | 7 | |||||||
| 13 | ✓ | 7 ± 4 | 6 | |||||||
| 14 | przed aktywacją | 204 ± 722 | 13 | |||||||
| 15 | po aktywacji | 294 ± 967 | 14 | |||||||
| 16 | przed aktywacją + batch size 128 | 12 ± 16 | 7 | |||||||
| 17 | po aktywacji + batch size 128 | 176 ± 827 | 8 | |||||||
| 18 | ✓ | ✓ | 5 ± 13 | 2 | ||||||
| 19 | ✓ | ✓ | ✓ | 3 ± 1 | 2 | |||||
| 20 | ✓ | ✓ | ✓ | przed aktywacją + batch size 128 | 36 ± 240 | 1 |
Z wybranych technik bardzo dobrze sprawdziła się zamiana Flatten na Global Max Pooling. Pomagało również data augmentation, szczególnie odbicie poziome i obroty. Z kolei dodanie Dropoutu i BatchNormalization powodowało dużą destabilizację accuracy oraz loss, co przekładało się na dużą średnią i odchylenie standardowe oraz wyższą medianę pomyłek modelu w stosunku do pozostałych wyników. Może to być spowodowane tym, że model nie jest zbyt skomplikowany. Próbą ustabilizowania Batch Normalization było zwiększenie rozmiaru batcha z 32 na 128.


Za najlepszy model uznajemy połączenie baseline + Global Max Pooling + Odbicie poziome + Obrót <= 180° + Batch Normalization przed aktywacją + batch size 128. Niestety jest tu jeszcze pewna niestabilność wprowadzona przez Batch Normalization, jak można zobaczyć na wykresach skrzypcowych powyżej, jednak mimo to temu modelowi udało się osiągnąć najniższą medianę pomyłek: 1.
Porównanie wyników – krzywe ROC, PR
Do porównywania modeli między sobą wykorzystuje się krzywe ROC i Precision-Recall wraz z polem pod krzywą odpowiednio: area under the ROC curve (AUC) oraz average precision (AP). Poniżej znajdują się krzywe ROC i PR dla baseline’u i najlepszego modelu – uśrednione oraz dla poszczególnych klas. Ponieważ oba modele popełniają stosunkowo mało błędów w klasyfikacji, to wykresy wyglądają idealnie i nie widać różnic między dwoma modelami.


Wyniki dla mniejszych zdjęć
Okazuje się jednak, że można tutaj wykorzystać krzywe ROC i PR do porównania modeli w innym kontekście. Jeśli w modelu jest Global Max Pooling, to może on przyjąć na wejście obraz o innym rozmiarze niż ten, który został ustalony przy tworzeniu modelu i był używany do treningu. Poniżej znajdują się krzywe ROC i PR dla najlepszego modelu i modelu z Global Max Pooling charakteryzujące klasyfikację obrazów o rozmiarze 32 x 32 piksele.


Prostszy model z Global Max Poolingiem radzi sobie lepiej przy mniejszych obrazach niż najlepszy model polegający widocznie na pewnych cechach obrazów, których nie ma na obrazach po zmniejszeniu. Widać to dodatkowo na poniższych wykresach – im mniejszy obraz, tym gorsze wyniki najlepszego modelu.

Podobnie jest z pozostałymi modelami z Global Max Poolingiem, tzn. radzą sobie lepiej ze zmniejszonymi obrazami niż najlepszy model, przy czym widać, że od pewnego rozmiaru – jak poniżej 48 x 48 px – wyniki modeli są już porównywalne.


Uczenie na wielu rozmiarach obrazów
Ponieważ okazało się, że najlepszy model radzi sobie najlepiej, ale tylko przy konkretnej rozdzielczości 64 x 64 px, można to poprawić poprzez trening najlepszego modelu na obrazach o różnych rozmiarach. Zamiast z góry przygotowanego zbioru treningowego do funkcji fit podajemy generator obrazów o losowo wybranej rozdzielczości na batch z zakresu 24 – 64 px (obraz jest skalowany przy użyciu albumentations) oraz steps_per_epoch:
def generate_images_various_sizes(X_train, y_train, batch_size):
bx = []
by = []
batch_count = 0
size = random.randrange(24, 64)
while True:
for i in range(X_train.shape[0]):
transform = A.Resize(size, size, p=1)
x = transform(image=X_train[i])['image']
y = y_train[i]
batch_count += 1
bx.append(x)
by.append(y)
if batch_count > batch_size:
bx = np.asarray(bx, dtype=np.float32)
by = np.asarray(by, dtype=np.float32)
yield (bx, by)
bx = []
by = []
batch_count = 0
size = random.randrange(24, 64)
batch_size = 32
model.fit(generate_images_various_sizes(X_train, y_train, batch_size), epochs=30, validation_data=(X_test, y_test), steps_per_epoch=X_train.shape[0]/batch_size)
Jak się można było spodziewać, najlepszy model trenowany na obrazach o różnym rozmiarze per batch osiąga już większą skuteczność predykcji obrazów o mniejszych rozmiarach:

Przykłady spoza zbioru
Sprawdźmy jeszcze, jak najlepszy model radzi sobie z obrazami spoza zbioru.

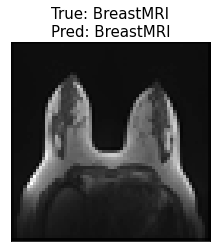
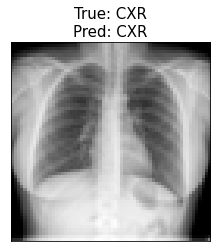
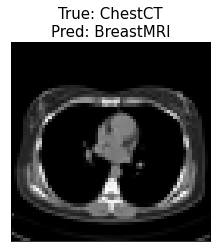
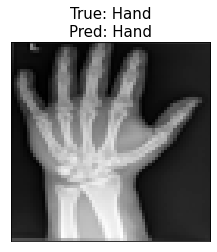
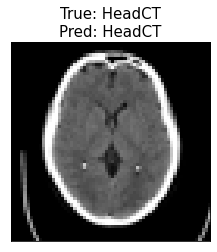
Model przewidział poprawnie 4 klasy, oprócz AbdomenCT i ChestCT, które uznał za BreastMRI. Niestety w tym wypadku trening najlepszego modelu przy użyciu generatora nie poprawił wyników i zarówno model trenowany na obrazach o jednej rozdzielczości 64 x 64 px, jak i model trenowany przy użyciu generatora obrazów o rozdzielczościach 24 – 64 px dają takie same predykcje dla powyższych obrazów.
Occlusion sensitivity
Jedną z metod wizualizowania, jak działa dany model i dlaczego podejmuje dane decyzje jest occlusion sensitivity. Polega na zakrywaniu kolejnych fragmentów obrazu danej klasy i sprawdzaniu, jak zmienia się prawdopodobieństwo tej klasy. Uzyskuje się w ten sposób heatmapę pokazującą, które regiony obrazu są najistotniejsze dla modelu przy klasyfikowaniu obrazu do konkretnej klasy. Rozdzielczość powstałej heatmapy zależy od rozmiaru ramki i kroku, czyli liczby pikseli, o jaką jest ona przesuwana. Poniżej zwizualizowanie, jak ramka o rozmiarze 16 x 16 pikseli przesuwa się co 8 pikseli po obrazie:

Wartości pikseli ramki przesłaniającej można wybrać dowolnie. To czy ramka jest koloru czarnego, czy białego będzie miało wpływ na wynik. Poniżej przedstawiona jest różnica między użyciem ramki czarnej i białej w occlusion sensitivity dla modelu Global Max Pooling. Dla ułatwienia w dalszej części wpisu będą przedstawione jedynie wyniki dla ramki czarnej.

Na przykładzie AbdomenCT można zobaczyć, że w przypadku poszczególnych modeli nieco inne regiony są istotne. Użycie Global Max Pooling sprawia, że niemal każdy fragment obrazu (przy odpowiednio dużym rozmiarze ramki) wpływa na predykcję modelu. Widać także, że w niektórych przypadkach rozmiar ramki jest zbyt mały, aby zmienić predykcję i heatmapy w ogóle nie ma; ramka o rozmiarze poniżej 4 x 4 piksele nie wpływa na predykcję żadnego z powyższych modeli.



Poniżej znajduje się occlusion sensitivity modelu wykorzystującego data augmentation – obrót <= 180° dla tego samego obrazu obróconego o różne kąty. W każdym przypadku dla modelu istotny jest środkowy fragment obrazu.



Jak się można spodziewać, dla najlepszego modelu inne regiony obrazów poszczególnych klas są kluczowe. Podobnie jak w zestawieniu powyżej również dla klas innych niż AbdomenCT dany rozmiar ramki (tu 16 x 16 pikseli) może być za mały, aby wpłynąć na wynik predykcji (jak przy BreastMRI). Zdjęcia tomografii komputerowej klatki piersiowej są podobne do zdjęć tomografii komputerowej jamy brzusznej i podobnie działa na nie occlusion sensitivity.

Pomyłki najlepszego modelu
Poniżej znajdują się przykładowe pomyłki, jakie popełniał najlepszy model. Środkowa kolumna obrazów przedstawia occlusion sensitivity i prawdopodobieństwo klasy prawdziwej, natomiast kolumna obrazów z prawej klasy fałszywie przewidzianej przez model. Ciekawy jest przykład CXR/Hand, gdzie wyraźnie widać fragment z lewej strony obrazu, który „nie bierze udziału” w przewidywaniu klasy prawdziwej, natomiast w przewidywaniu klasy fałszywej jest istotny. Na oryginalnym obrazie jest to fragment jednolity, na podstawie którego człowiek nie podejmowałby decyzji, z jakim obrazem ma do czynienia.

Podobnie do powyższego przypadku Hand/CXR wyglądają przykładowe pomyłki najlepszego modelu trenowanego na generatorze obrazów o różnych rozmiarach. Widać poszczególne fragmenty obrazu, które są decydujące przy sklasyfikowaniu obrazu do klasy fałszywej i prawdziwej (która jest w każdym przypadku drugim wyborem modelu).
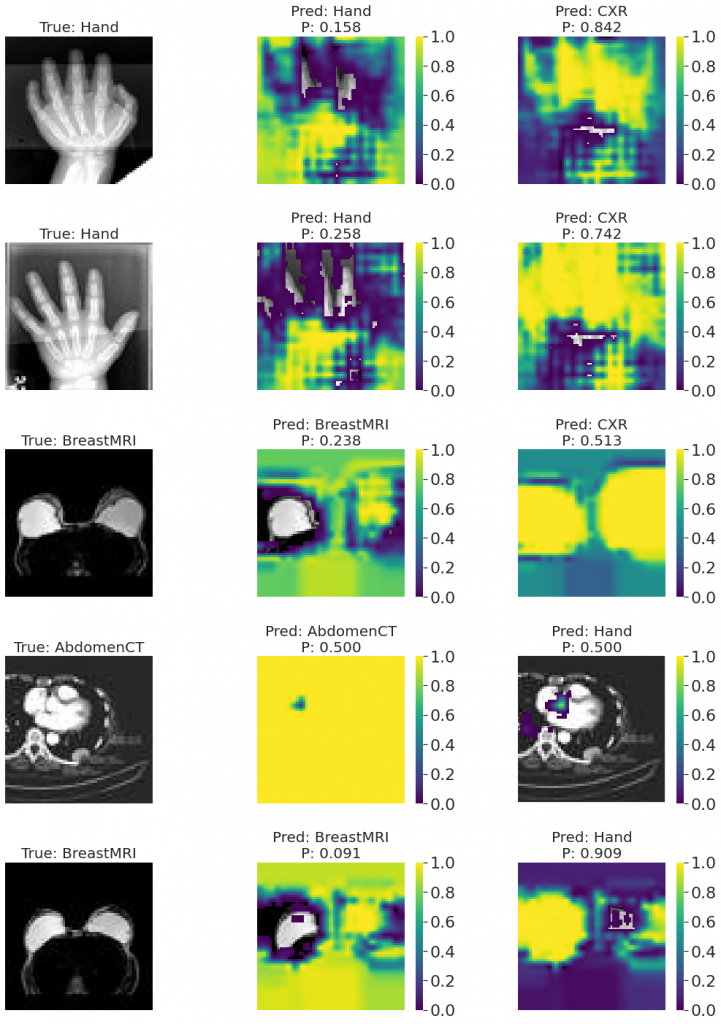
Occlusion jako data augmentation podczas uczenia
Tak jak w przypadku polepszenia działania modelu poprzez trening na różnych rozdzielczościach per batch, można także wpłynąć na wynik occlusion sensitivity poprzez trening na generatorze obrazów. W tym przypadku generowane są obrazy z przysłoniętym losowo wybranym fragmentem obrazu (rozmiar ramki przysłaniającej podczas treningu: 16 x 16 px). Przy okazji warto zaznaczyć, że taki model popełnia więcej pomyłek na zbiorze testowym, który nie zawiera obrazów z occlusion niż model nietrenowany na generatorze.
Na poniższych przykładach widać, że rozmiar ramki 16 x 16 pikseli jest teraz zbyt mały, aby wpływać na predykcję – poza modelem Global Max Pooling, dla którego taka ramka zmienia wynik, jednak w mniejszym stopniu niż dla modelu nietrenowanego na generatorze. Przedstawione są również wyniki occlusion sensitivity dla najmniejszego rozmiaru ramki, który wpływa na predykcję danego modelu trenowanego na generatorze obrazów z occlusion. Okazuje się, że dla większości z poniższych modeli ramka musi przesłaniać znaczną część obrazu, aby zmieniło to predykcję.


Wizualizacje z użyciem t-SNE
Inną techniką wizualizacji działania modelu jest t-SNE (t-Distributed Stochastic Neighbour Embedding). Jest to metoda redukcji liczby wymiarów. Wizualizacja 2D wielowymiarowej reprezentacji cech na wyjściu warstwy Global Max Pooling pozwala zobaczyć, które obiekty są według danego modelu podobne.

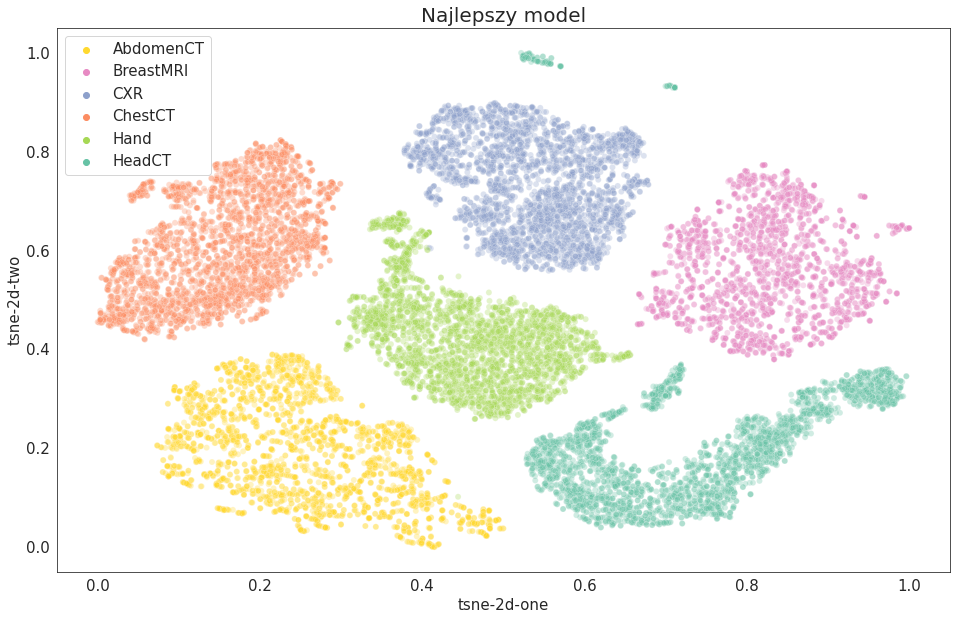


Każdy powyższy model dość podobnie klasyfikuje obrazy, a klasy są wyraźnie rozdzielone na poszczególne klastry. Jest parę różnic. Da się zauważyć, że w przypadku modelu z Global Max Poolingiem jeden przykład CXR znalazł się bliżej klastra Hand. Różna jest również w każdym przypadku liczba przykładów HeadCT, które znajdują poza 'głównym’ klastrem tej klasy.
t-SNE dla mniejszych obrazów na wejściu
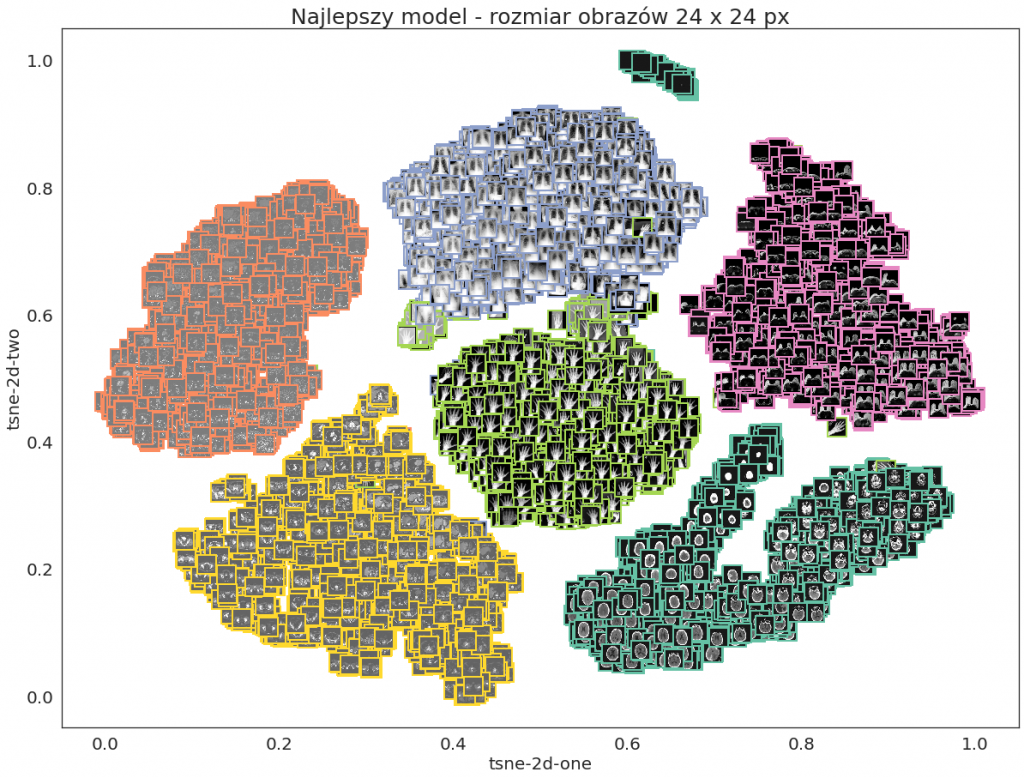
Porównajmy jeszcze wizualizacje t-SNE dla obrazów mniejszych niż 64 x 64 px. Podobnie jak powyżej widać, że klasy są rozdzielone na poszczególne klastry, przy czym w niektórych przypadkach część przykładów jest słabiej rozdzielona (jak na przykład dla najlepszego modelu – rozmiar obrazów 24 x 24 px, gdzie grupka obrazów Hand znajduje się przy klastrze CXR).








Zamiast punktów na wykresie punktowym można pokazać obrazy, które danym punktom odpowiadają. Co prawda granice klastrów mogą okazać się mniej wyraźne (szczególnie w przypadku większych obrazów, które na wykresie będą zajmowały więcej miejsca) – w razie wątpliwości można poniższe wykresy porównać z odpowiednimi wykresami powyżej. Dla ułatwienia obrazy mają ramkę w kolorze odpowiadającym ich klasie. Na takim wykresie z obrazami zamiast punktów można zobaczyć, które obrazy odstają od głównych klastrów swoich klas. Poniżej widać, że z dala od głównej grupy HeadCT znajdują się obrazy, na których w ogóle nie widać czaszki lub jest ona małym punkcikiem (może to być przekrój na przykład na wysokości czubka głowy). Na wizualizacji z obrazami 24 x 24 px widać, że przypadki Hand znajdujące się w grupie CXR lub blisko niej to obrazy z jasnym tłem.
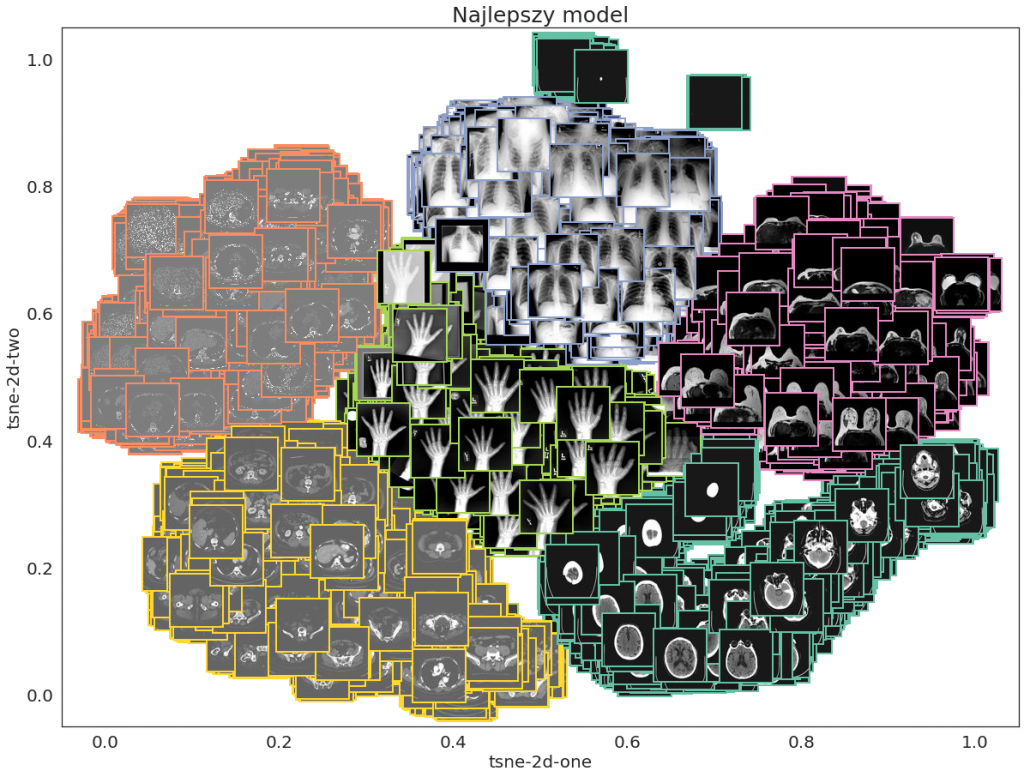


t-SNE grid
Szczególnym przypadkiem wizualizacji z użyciem t-SNE jest wizualizacja obrazów w gridzie. Podobnie jak w powyższym przypadku wielowymiarowa reprezentacja cech na wyjściu warstwy Global Max Pooling jest sprowadzana do dwóch wymiarów, przy czym zamiast wykresu punktowego w dwuwymiarowej przestrzeni t-SNE obrazy są układane w kwadratowej siatce przy użyciu algorytmu Jonkera-Volgenanta. W takiej mozaice obrazy podobne są położone blisko siebie. Poniżej kilka przykładów Hand o kolorze tła innym niż czarne znajduje się obok CXR, do którego są podobne wizualnie. Widać, że jeden przypadek Hand o szarym tle znalazł się nawet dalej od innych przykładów swojej klasy, a bliżej przykładów ChestCT, które mają podobne tło.

Można się pokusić o umieszczenie w gridzie niemal wszystkich obrazów ze zbioru testowego (√17687 ≈ 132 – zaokrąglając w dół, aby nie było pustych miejsc na mozaice; zatem mozaika będzie miała wymiar 132 x 132 obrazy). Aby lepiej było widać, która klasa zajmuje dany obszar, można zamienić obrazy na kolory.



Na mozaice kolorowej na pierwszy rzut oka widać, że nie wszystkie obrazy niektórych klas są położone obok siebie, tak jak niektóre przykłady HeadCT znajdujące się w innej części mozaiki niż większość obrazów tej klasy oraz przykład Hand nieznajdujący się obok innych przykładów swojej klasy, a pośród przykładów AbdomenCT. Nakładając na siebie obie powyższe mozaiki (kolory pomogą rozpoznać klasę w razie wątpliwości), a następnie powiększając obraz, można zobaczyć, które konkretnie przypadki odstają od pozostałych przykładów swoich klas.


t-SNE grid – RasterFairy
Punkty z przestrzeni t-SNE można ułożyć również w inne kształty niż kwadrat, do czego można wykorzystać bibliotekę RasterFairy. Poza kształtami regularnymi, np. koło, jest możliwość podania jako szablon maski binarnej o dowolnym kształcie. Poniżej znajdują się przykładowe wizualizacje. Zostały wykonane tylko dla około 1/5 zbioru testowego, ponieważ w przypadku całości zbioru obliczenia były zbyt czaso- i zasobochłonne; z tego też względu klasy mogą mieć inne położenie w przestrzeni niż na wykresach powyżej.



Wnioski
Medical MNIST jest w miarę prostym zbiorem do analizowania i podstawowej klasyfikacji, ale może stanowić dobry punkt wyjścia do dalszego działania. Szkoda jedynie, że nie mamy tu 10 klas jak w oryginalnym MNIST i innych jego pochodnych jak na przykład Fashion MNIST czy notMNIST, aby skojarzenie obejmowało szerszy kontekst niż tylko nazwę i prostotę zbioru.
Powyższy projekt powstawał głównie na Google Colab. Jednak na etapie trenowania poszczególnych modeli darmowa wersja Google Colaboratory okazała się niewystarczająca. Po jakimś czasie korzystania z GPU Colab blokuje możliwość jego używania i należy odczekać, aż znowu GPU będzie dostępne. Oczywiście nadal można korzystać z CPU, jednak jest to bardzo czasochłonne w przypadku danych obrazowych, więc trening został przeniesiony na Amazon EC2 (g4dn.2xlarge z 1 GPU).
Eksperymenty pokazały, że można poprawić wynik różnymi technikami, na przykład przez data augmentation – to jest dość istotne w medycynie, gdyż często występuje tu problem małej ilości danych i brak danych oznaczonych. W ramach rozszerzenia projektu można by rozważyć również inne metody data augmentation, jak na przykład zmiana kontrastu lub innych parametrów obrazu. Mogłoby to w szczególności polepszyć rozpoznawanie przez model obrazów spoza zbioru. Pomocny bardzo jest również Global Max Pooling, który zapobiega przeuczeniu i generuje mniej parametrów niż Flatten, dzięki czemu model jest mniejszy. Batch Normalization zastosowany przed funkcją aktywacji wprowadzał trochę niestabilności, jednak mimo to również poprawiał wynik. Co więcej, model z Global Max Poolingiem można wytrenować na obrazach o różnych rozdzielczościach per batch, aby był skuteczniejszy również dla obrazów mniejszych niż 64 x 64 piksele.
Do analizy modelu przydaje się occlusion sensitivity. Można zobaczyć, że pewne obszary danego obrazu są istotne przy klasyfikacji i ich przysłonięcie zmienia predykcję modelu. Obrazy w zbiorze Medical MNIST są dość małe (64 x 64 piksele), więc niestety nie można wyciągnąć tutaj zbyt wielu wniosków na podstawie samego occlusion sensitivity, które działa dokładniej i efektowniej na obrazach o większych rozmiarach. Do wizualizacji działania modelu pomocne jest również t-SNE. Poza occlusion sensitivity i t-SNE do analizy modelu można by dodatkowo użyć innego narzędzia, na przykład SHAP – niestety obecnie nie jest on jeszcze kompatybilny z Tensorflow 2.